{x}
blog image

Parallel Courses III

You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given a 2D integer array relations where relations[j] = [prevCoursej, nextCoursej] denotes that course prevCoursej has to be completed before course nextCoursej (prerequisite relationship). Furthermore, you are given a 0-indexed integer array time where time[i] denotes how many months it takes to complete the (i+1)th course.

You must find the minimum number of months needed to complete all the courses following these rules:

  • You may start taking a course at any time if the prerequisites are met.
  • Any number of courses can be taken at the same time.

Return the minimum number of months needed to complete all the courses.

Note: The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).

 

Example 1:

Input: n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
Output: 8
Explanation: The figure above represents the given graph and the time required to complete each course. 
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.

Example 2:

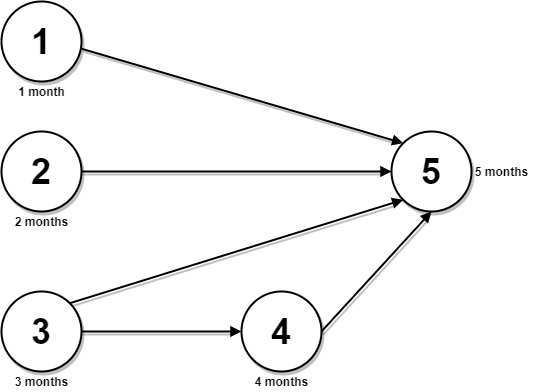
Input: n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
Output: 12
Explanation: The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.

 

Constraints:

  • 1 <= n <= 5 * 104
  • 0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)
  • relations[j].length == 2
  • 1 <= prevCoursej, nextCoursej <= n
  • prevCoursej != nextCoursej
  • All the pairs [prevCoursej, nextCoursej] are unique.
  • time.length == n
  • 1 <= time[i] <= 104
  • The given graph is a directed acyclic graph.

Solution Explanation: Parallel Courses III

This problem asks for the minimum time to complete all courses, given prerequisites and individual course durations. We can solve this using Topological Sort and Dynamic Programming.

1. Topological Sort:

A topological sort arranges nodes (courses) in a directed acyclic graph (DAG) such that for every directed edge from node A to node B, node A appears before node B in the ordering. This is crucial because a course cannot be started until all its prerequisites are finished.

2. Dynamic Programming:

Dynamic programming helps us efficiently calculate the minimum completion time. We use an array f where f[i] represents the earliest time course i can be completed.

Algorithm:

  1. Build the graph: Create an adjacency list g representing the course dependencies. g[i] contains a list of courses that depend on course i. Also, create an indegree array to store the number of prerequisites for each course.

  2. Find starting nodes: Identify courses with an in-degree of 0 (no prerequisites). These are the courses we can start immediately. Add these to a queue q.

  3. Topological Traversal: Process the queue. For each course i removed from the queue:

    • Calculate the earliest completion time for i: f[i] = time[i]. If i has prerequisites, we need to consider the maximum completion time among its prerequisites.
    • Update the earliest completion times of dependent courses (j in g[i]): f[j] = max(f[j], f[i] + time[j]).
    • Decrement the in-degree of all dependent courses. If a course's in-degree becomes 0, add it to the queue.

  4. Find the final answer: The maximum value in f represents the minimum time to complete all courses.

Time Complexity: O(V + E), where V is the number of courses (nodes) and E is the number of prerequisites (edges). This is because we visit each node and edge once during the topological sort and DP steps.

Space Complexity: O(V + E) for storing the graph, in-degree array, and DP array.

Code Examples (Python):

from collections import defaultdict, deque
 
def minimumTime(n: int, relations: list[list[int]], time: list[int]) -> int:
    g = defaultdict(list)
    indegree = [0] * n
    for u, v in relations:
        g[u - 1].append(v - 1)  # Adjust for 0-based indexing
        indegree[v - 1] += 1
 
    q = deque()
    f = [0] * n  # Earliest completion time for each course
    for i in range(n):
        if indegree[i] == 0:
            q.append(i)
            f[i] = time[i]
 
    ans = 0
    while q:
        u = q.popleft()
        ans = max(ans, f[u])
        for v in g[u]:
            f[v] = max(f[v], f[u] + time[v])
            indegree[v] -= 1
            if indegree[v] == 0:
                q.append(v)
 
    return ans

Other languages (Java, C++, Go, TypeScript) follow a similar structure, adapting the data structures and syntax accordingly. The core algorithm remains consistent across all languages.