{x}
blog image

Second Minimum Time to Reach Destination

A city is represented as a bi-directional connected graph with n vertices where each vertex is labeled from 1 to n (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself. The time taken to traverse any edge is time minutes.

Each vertex has a traffic signal which changes its color from green to red and vice versa every change minutes. All signals change at the same time. You can enter a vertex at any time, but can leave a vertex only when the signal is green. You cannot wait at a vertex if the signal is green.

The second minimum value is defined as the smallest value strictly larger than the minimum value.

  • For example the second minimum value of [2, 3, 4] is 3, and the second minimum value of [2, 2, 4] is 4.

Given n, edges, time, and change, return the second minimum time it will take to go from vertex 1 to vertex n.

Notes:

  • You can go through any vertex any number of times, including 1 and n.
  • You can assume that when the journey starts, all signals have just turned green.

 

Example 1:

        
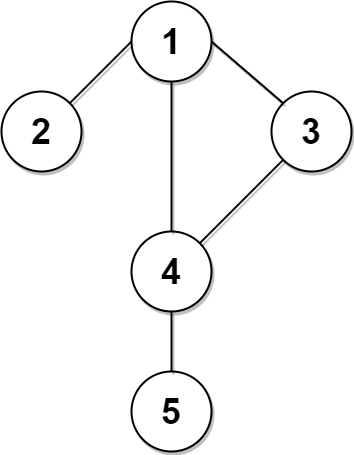
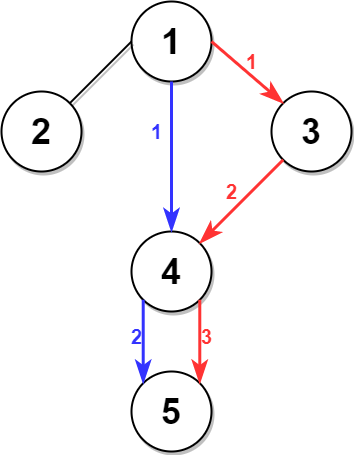
Input: n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
Output: 13
Explanation:
The figure on the left shows the given graph.
The blue path in the figure on the right is the minimum time path.
The time taken is:
- Start at 1, time elapsed=0
- 1 -> 4: 3 minutes, time elapsed=3
- 4 -> 5: 3 minutes, time elapsed=6
Hence the minimum time needed is 6 minutes.

The red path shows the path to get the second minimum time.
- Start at 1, time elapsed=0
- 1 -> 3: 3 minutes, time elapsed=3
- 3 -> 4: 3 minutes, time elapsed=6
- Wait at 4 for 4 minutes, time elapsed=10
- 4 -> 5: 3 minutes, time elapsed=13
Hence the second minimum time is 13 minutes.

Example 2:

Input: n = 2, edges = [[1,2]], time = 3, change = 2
Output: 11
Explanation:
The minimum time path is 1 -> 2 with time = 3 minutes.
The second minimum time path is 1 -> 2 -> 1 -> 2 with time = 11 minutes.

 

Constraints:

  • 2 <= n <= 104
  • n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)
  • edges[i].length == 2
  • 1 <= ui, vi <= n
  • ui != vi
  • There are no duplicate edges.
  • Each vertex can be reached directly or indirectly from every other vertex.
  • 1 <= time, change <= 103

Solution Explanation:

This problem asks for the second minimum time to reach a destination node in a graph, considering traffic signals at each node. The solution uses a modified Breadth-First Search (BFS) algorithm to find both the minimum and second minimum times.

Approach:

  1. Graph Representation: The input edges is used to create an adjacency list (g) representing the graph. This allows efficient access to neighbors of each node.

  2. BFS with Distance Tracking: A BFS is performed starting from node 1. Instead of tracking just the minimum distance, we maintain a dist array of size n+1 where dist[i][0] stores the minimum time to reach node i, and dist[i][1] stores the second minimum time. Initially, dist[i][0] and dist[i][1] are set to infinity.

  3. Queue Management: The BFS queue q stores tuples of (node, time). The time represents the total time taken to reach that node.

  4. Distance Update: During BFS, when a neighbor v of the current node u is visited:

    • If d + 1 (the time to reach v from u) is less than the current minimum time (dist[v][0]), update dist[v][0] and add (v, d + 1) to the queue.
    • If dist[v][0] < d + 1 < dist[v][1] (meaning d + 1 is greater than the minimum but less than the second minimum), update dist[v][1] and add (v, d + 1) to the queue.

  5. Signal Time Calculation: Once the BFS completes, dist[n][1] contains the second minimum number of edges to reach node n. The final answer is calculated by considering the time to traverse each edge and adding waiting time at red signals. The waiting time is calculated based on whether the time at a node is an odd or even multiple of change.

Time Complexity:

The BFS algorithm visits each edge at most twice (once for the minimum and once for the second minimum). Therefore, the time complexity is O(E), where E is the number of edges in the graph. In the worst case, E can be O(V^2), where V is the number of vertices (nodes).

Space Complexity:

The space complexity is O(V) due to the dist array and the BFS queue, both of which store information about each node.

Code Explanation (Python):

The Python code efficiently implements the algorithm described above using a defaultdict for the adjacency list and deque for the BFS queue. The signal time calculation is handled within the final loop.

Code Explanation (Java):

The Java code uses ArrayList for the adjacency list and LinkedList for the BFS queue. The logic for handling distances and signal times remains the same as the Python version.

In both languages, the code clearly demonstrates the steps outlined in the approach section, making it easy to understand and follow the solution.