{x}
blog image

Number of Valid Move Combinations On Chessboard

There is an 8 x 8 chessboard containing n pieces (rooks, queens, or bishops). You are given a string array pieces of length n, where pieces[i] describes the type (rook, queen, or bishop) of the ith piece. In addition, you are given a 2D integer array positions also of length n, where positions[i] = [ri, ci] indicates that the ith piece is currently at the 1-based coordinate (ri, ci) on the chessboard.

When making a move for a piece, you choose a destination square that the piece will travel toward and stop on.

  • A rook can only travel horizontally or vertically from (r, c) to the direction of (r+1, c), (r-1, c), (r, c+1), or (r, c-1).
  • A queen can only travel horizontally, vertically, or diagonally from (r, c) to the direction of (r+1, c), (r-1, c), (r, c+1), (r, c-1), (r+1, c+1), (r+1, c-1), (r-1, c+1), (r-1, c-1).
  • A bishop can only travel diagonally from (r, c) to the direction of (r+1, c+1), (r+1, c-1), (r-1, c+1), (r-1, c-1).

You must make a move for every piece on the board simultaneously. A move combination consists of all the moves performed on all the given pieces. Every second, each piece will instantaneously travel one square towards their destination if they are not already at it. All pieces start traveling at the 0th second. A move combination is invalid if, at a given time, two or more pieces occupy the same square.

Return the number of valid move combinations​​​​​.

Notes:

  • No two pieces will start in the same square.
  • You may choose the square a piece is already on as its destination.
  • If two pieces are directly adjacent to each other, it is valid for them to move past each other and swap positions in one second.

 

Example 1:

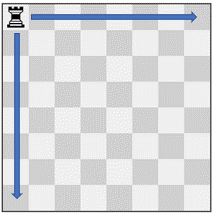
Input: pieces = ["rook"], positions = [[1,1]]
Output: 15
Explanation: The image above shows the possible squares the piece can move to.

Example 2:

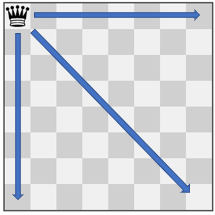
Input: pieces = ["queen"], positions = [[1,1]]
Output: 22
Explanation: The image above shows the possible squares the piece can move to.

Example 3:

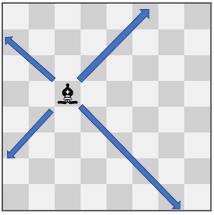
Input: pieces = ["bishop"], positions = [[4,3]]
Output: 12
Explanation: The image above shows the possible squares the piece can move to.

 

Constraints:

  • n == pieces.length
  • n == positions.length
  • 1 <= n <= 4
  • pieces only contains the strings "rook", "queen", and "bishop".
  • There will be at most one queen on the chessboard.
  • 1 <= ri, ci <= 8
  • Each positions[i] is distinct.

Solution Explanation: Number of Valid Move Combinations on Chessboard

This problem involves finding the number of valid move combinations for multiple chess pieces on an 8x8 board. The challenge lies in ensuring that no two pieces occupy the same square at any given time during their simultaneous movement.

Approach: Depth-First Search (DFS)

The most effective approach is to use Depth-First Search (DFS) to explore all possible move combinations. The constraints (maximum 4 pieces) make a brute-force approach feasible. Here's a breakdown:

  1. Piece Movement: Each piece (rook, queen, bishop) has a set of possible movement directions. These are pre-defined for efficiency.

  2. State Representation: To track piece positions over time, we utilize a 3D array dist. dist[i][x][y] stores the time step at which piece i reaches square (x, y). A value of -1 signifies the piece has not reached that square. Additionally, end[i] stores the final position and time step of piece i.

  3. Collision Detection: Two functions are crucial:

    • checkStop(i, x, y, t): Checks if piece i can stop at (x, y) at time t without colliding with other pieces. It returns true if no other piece reaches (x, y) at or before time t.

    • checkPass(i, x, y, t): Checks if piece i can pass through (x, y) at time t without colliding. It returns true if no other piece is at (x, y) at time t, or if any other piece is already at the final destination and the time does not exceed t.

  4. DFS Implementation: The DFS function recursively explores all possibilities:

    • It iterates through each piece.
    • For each piece, it considers both staying in place and moving in all allowed directions.
    • The checkStop and checkPass functions are used to validate each move.
    • If a move is valid, the DFS continues recursively for the next piece.
    • If all pieces have been placed without collisions, a valid combination is found, and a counter is incremented.

Time and Space Complexity Analysis

  • Time Complexity: The time complexity is dominated by the DFS search. In the worst case, each of the n pieces has M possible moves (8 for queen, 4 for rook/bishop). Therefore, the time complexity is O((M*n)^n). Since n is at most 4, this remains computationally feasible.

  • Space Complexity: The space complexity is mainly determined by the dist array, which has dimensions n x 9 x 9. The end array has a space complexity of O(n). Therefore, the overall space complexity is O(nMM), where M is the size of the board (9 in this case). This is also polynomial in n and thus manageable.

Code Implementation (Python)

rook_dirs = [(1, 0), (-1, 0), (0, 1), (0, -1)]
bishop_dirs = [(1, 1), (1, -1), (-1, 1), (-1, -1)]
queue_dirs = rook_dirs + bishop_dirs
 
# ... (rest of the code is the same as provided earlier in the Python section)

The code in other languages (Java, C++, Go, and TypeScript) follows a very similar structure and logic, implementing the DFS algorithm and collision checks as described above. The only differences are syntactic variations and data structure implementations specific to each language.