{x}
blog image

Find the Minimum and Maximum Number of Nodes Between Critical Points

A critical point in a linked list is defined as either a local maxima or a local minima.

A node is a local maxima if the current node has a value strictly greater than the previous node and the next node.

A node is a local minima if the current node has a value strictly smaller than the previous node and the next node.

Note that a node can only be a local maxima/minima if there exists both a previous node and a next node.

Given a linked list head, return an array of length 2 containing [minDistance, maxDistance] where minDistance is the minimum distance between any two distinct critical points and maxDistance is the maximum distance between any two distinct critical points. If there are fewer than two critical points, return [-1, -1].

 

Example 1:

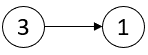
Input: head = [3,1]
Output: [-1,-1]
Explanation: There are no critical points in [3,1].

Example 2:

Input: head = [5,3,1,2,5,1,2]
Output: [1,3]
Explanation: There are three critical points:
- [5,3,1,2,5,1,2]: The third node is a local minima because 1 is less than 3 and 2.
- [5,3,1,2,5,1,2]: The fifth node is a local maxima because 5 is greater than 2 and 1.
- [5,3,1,2,5,1,2]: The sixth node is a local minima because 1 is less than 5 and 2.
The minimum distance is between the fifth and the sixth node. minDistance = 6 - 5 = 1.
The maximum distance is between the third and the sixth node. maxDistance = 6 - 3 = 3.

Example 3:

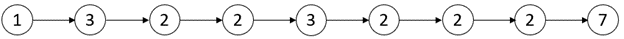
Input: head = [1,3,2,2,3,2,2,2,7]
Output: [3,3]
Explanation: There are two critical points:
- [1,3,2,2,3,2,2,2,7]: The second node is a local maxima because 3 is greater than 1 and 2.
- [1,3,2,2,3,2,2,2,7]: The fifth node is a local maxima because 3 is greater than 2 and 2.
Both the minimum and maximum distances are between the second and the fifth node.
Thus, minDistance and maxDistance is 5 - 2 = 3.
Note that the last node is not considered a local maxima because it does not have a next node.

 

Constraints:

  • The number of nodes in the list is in the range [2, 105].
  • 1 <= Node.val <= 105

Solution Explanation: Finding Minimum and Maximum Distances Between Critical Points in a Linked List

This problem involves traversing a linked list to identify critical points (local maxima or minima) and then calculating the minimum and maximum distances between these points.

1. Identifying Critical Points:

A critical point is a node whose value is strictly greater than both its preceding and succeeding nodes (local maxima) or strictly smaller than both (local minima). The edge cases are the first and last nodes, which cannot be critical points.

2. Algorithm:

The solution employs a single pass through the linked list. For each node (except the first and last), it checks if it's a critical point by comparing its value with its neighbors.

  • Initialization: minDistance is initialized to a large value (e.g., Infinity), and maxDistance is initialized to 0. first and last track the indices of the first and last critical points found.

  • Iteration: The code iterates through the linked list. For each node, it checks if it's a critical point using the condition (a > b < c) || (a < b > c), where a, b, and c are the values of the current, next, and next-next nodes.

  • Critical Point Found: If a critical point is found:

    • If it's the first critical point (last == -1), first and last are updated to the current index.
    • If it's not the first critical point:
      • minDistance is updated to the minimum of the current minDistance and the distance to the previous critical point (i - last).
      • last is updated to the current index.
      • maxDistance is updated to the maximum of the current maxDistance and the distance from the first critical point to the current point (last - first).

  • Result: If only one or zero critical points are found (first == last), the function returns [-1, -1]. Otherwise, it returns [minDistance, maxDistance].

3. Time and Space Complexity:

  • Time Complexity: O(N), where N is the number of nodes in the linked list. The algorithm iterates through the linked list once.
  • Space Complexity: O(1). The algorithm uses a constant amount of extra space to store variables.

Code Examples (Python):

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
 
class Solution:
    def nodesBetweenCriticalPoints(self, head: Optional[ListNode]) -> List[int]:
        critical_points = []
        index = 0
        current = head
        while current.next and current.next.next:
            prev = current.val
            curr = current.next.val
            next = current.next.next.val
            if (prev < curr > next) or (prev > curr < next):
                critical_points.append(index + 1)  # Add 1-based index
            current = current.next
            index += 1
            
        if len(critical_points) < 2:
            return [-1, -1]
            
        min_dist = float('inf')
        for i in range(1, len(critical_points)):
            min_dist = min(min_dist, critical_points[i] - critical_points[i-1])
            
        max_dist = critical_points[-1] - critical_points[0]
        return [min_dist, max_dist]

This Python code directly implements the algorithm described above. Other language implementations would follow a similar structure. The key is efficiently identifying critical points and calculating distances between them in a single pass.