- {x}
- Sort Linked List Already Sorted Using Absolute Values
- Number of Valid Words in a Sentence
- Next Greater Numerically Balanced Number
- Count Nodes With the Highest Score
- Parallel Courses III
- The Category of Each Member in the Store
- Minimum Cost to Separate Sentence Into Rows
- Kth Distinct String in an Array
- Two Best Non-Overlapping Events
- Plates Between Candles
- Number of Valid Move Combinations On Chessboard
- Smallest Index With Equal Value
- Find the Minimum and Maximum Number of Nodes Between Critical Points
- Minimum Operations to Convert Number
- Check if an Original String Exists Given Two Encoded Strings
- Number of Spaces Cleaning Robot Cleaned
- Count Vowel Substrings of a String
- Read More...

Two Best Non-Overlapping Events
You are given a 0-indexed 2D integer array of events where events[i] = [startTimei, endTimei, valuei]. The ith event starts at startTimei and ends at endTimei, and if you attend this event, you will receive a value of valuei. You can choose at most two non-overlapping events to attend such that the sum of their values is maximized.
Return this maximum sum.
Note that the start time and end time is inclusive: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time t, the next event must start at or after t + 1.
Example 1:
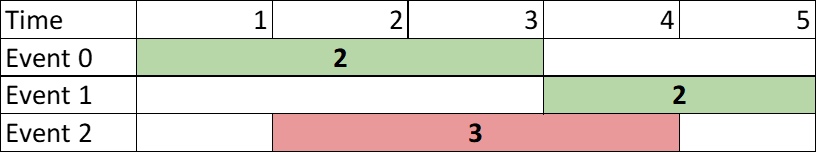
Input: events = [[1,3,2],[4,5,2],[2,4,3]] Output: 4 Explanation: Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.
Example 2:

Input: events = [[1,3,2],[4,5,2],[1,5,5]] Output: 5 Explanation: Choose event 2 for a sum of 5.
Example 3:

Input: events = [[1,5,3],[1,5,1],[6,6,5]] Output: 8 Explanation: Choose events 0 and 2 for a sum of 3 + 5 = 8.
Constraints:
2 <= events.length <= 105events[i].length == 31 <= startTimei <= endTimei <= 1091 <= valuei <= 106
Solution Explanation:
This problem asks us to find the maximum sum of values from at most two non-overlapping events. The solution uses a combination of sorting and binary search for efficient computation.
Approach:
-
Sort Events: First, we sort the
eventsarray by their start times. This allows us to efficiently find non-overlapping events later. -
Calculate Maximum Value from Later Events: We create a
farray.f[i]stores the maximum sum of values that can be obtained by attending events starting from indexionwards. We compute this array iteratively, from right to left:f[i] = max(f[i+1], events[i][2]). This means the maximum value from indexionwards is either the maximum value from indexi+1onwards, or the value of eventiitself. -
Iterate and Find Maximum Sum: We iterate through the sorted
eventsarray. For each event:- We calculate its value (
v). - We use binary search to find the index (
idx) of the first event that starts after the current event ends (events[i][1]). This efficiently identifies the range of events that don't overlap with the current event. - If such an event exists (
idx < n), we add the maximum value from that index onwards (f[idx]) tov. - We update
ans(the maximum sum found so far) to be the maximum ofansandv.
- We calculate its value (
-
Return Result: The
ansvariable holds the maximum sum of values from at most two non-overlapping events.
Time Complexity Analysis:
- Sorting the events takes O(N log N) time, where N is the number of events.
- Constructing the
farray takes O(N) time. - Iterating through the events and performing binary search for each event takes O(N log N) time.
Therefore, the overall time complexity of this solution is O(N log N), dominated by the sorting and binary search steps.
Space Complexity Analysis:
The space complexity is O(N), primarily due to the f array used to store the maximum values from suffixes of the sorted events.
Code Explanation (Python):
The Python code directly implements the approach described above. Let's break down the key parts:
class Solution:
def maxTwoEvents(self, events: List[List[int]]) -> int:
events.sort() # Sort events by start time
n = len(events)
f = [events[-1][2]] * n # Initialize f array with the last event's value
for i in range(n - 2, -1, -1): # Calculate f array from right to left
f[i] = max(f[i + 1], events[i][2])
ans = 0
for _, e, v in events: # Iterate through events
idx = bisect_right(events, e, key=lambda x: x[0]) #Binary search for non-overlapping event
if idx < n:
v += f[idx] # Add maximum value from non-overlapping events
ans = max(ans, v) # Update maximum sum
return ansThe bisect_right function from the bisect module efficiently finds the insertion point for a value in a sorted list, effectively performing the binary search. The lambda function lambda x: x[0] specifies that the comparison should be based on the start time (the first element) of each event.
The Java, C++, and Go solutions follow a very similar structure and logic, with the primary differences lying in syntax and standard library functions used for sorting and binary search. They all achieve the same time and space complexity.