{x}
blog image

Plates Between Candles

There is a long table with a line of plates and candles arranged on top of it. You are given a 0-indexed string s consisting of characters '*' and '|' only, where a '*' represents a plate and a '|' represents a candle.

You are also given a 0-indexed 2D integer array queries where queries[i] = [lefti, righti] denotes the substring s[lefti...righti] (inclusive). For each query, you need to find the number of plates between candles that are in the substring. A plate is considered between candles if there is at least one candle to its left and at least one candle to its right in the substring.

  • For example, s = "||**||**|*", and a query [3, 8] denotes the substring "*||**|". The number of plates between candles in this substring is 2, as each of the two plates has at least one candle in the substring to its left and right.

Return an integer array answer where answer[i] is the answer to the ith query.

 

Example 1:

ex-1 
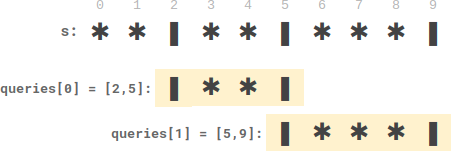
Input: s = "**|**|***|", queries = [[2,5],[5,9]]
Output: [2,3]
Explanation:
- queries[0] has two plates between candles.
- queries[1] has three plates between candles.

Example 2:

ex-2 
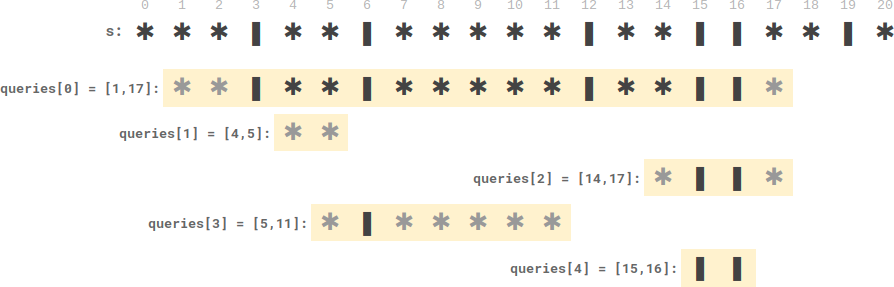
Input: s = "***|**|*****|**||**|*", queries = [[1,17],[4,5],[14,17],[5,11],[15,16]]
Output: [9,0,0,0,0]
Explanation:
- queries[0] has nine plates between candles.
- The other queries have zero plates between candles.

 

Constraints:

  • 3 <= s.length <= 105
  • s consists of '*' and '|' characters.
  • 1 <= queries.length <= 105
  • queries[i].length == 2
  • 0 <= lefti <= righti < s.length

Solution Explanation

This problem asks to find the number of plates between candles for each query range in a string. The solution leverages prefix sums and pre-computed arrays to efficiently answer multiple queries.

Approach:

  1. Prefix Sum: A presum array is created to store the cumulative sum of plates encountered so far. presum[i] represents the total number of plates from index 0 to i-1. This allows for constant-time calculation of the number of plates in any range.

  2. Nearest Candle Arrays: Two arrays, left and right, are created. left[i] stores the index of the nearest candle to the left of index i, and right[i] stores the index of the nearest candle to the right of index i. These arrays are computed using single linear scans of the string.

  3. Query Processing: For each query [left_i, right_i]:

    • The nearest candles to the left of left_i (i) and to the right of right_i (j) are found using the left and right arrays.
    • If both i and j are valid (meaning candles exist within the query range and i < j), then the number of plates between these candles is calculated as presum[j] - presum[i + 1]. This is the efficient part enabled by the prefix sum.

Time Complexity Analysis:

  • Creating presum array: O(N), where N is the length of the string.
  • Creating left and right arrays: O(N) each, for a total of O(N).
  • Processing queries: O(Q), where Q is the number of queries. Each query takes constant time O(1) due to the pre-computed arrays.

Therefore, the overall time complexity is O(N + Q).

Space Complexity Analysis:

  • presum, left, right arrays: O(N) each.
  • ans array: O(Q).

The overall space complexity is O(N + Q).

Code Explanation (Python3):

class Solution:
    def platesBetweenCandles(self, s: str, queries: List[List[int]]) -> List[int]:
        n = len(s)
        presum = [0] * (n + 1)  # Prefix sum array
        for i, c in enumerate(s):
            presum[i + 1] = presum[i] + (c == '*')
 
        left, right = [0] * n, [0] * n #Nearest candle arrays
        l = r = -1
        for i, c in enumerate(s):
            if c == '|':
                l = i
            left[i] = l
        for i in range(n - 1, -1, -1):
            if s[i] == '|':
                r = i
            right[i] = r
 
        ans = [0] * len(queries) #result array
        for k, (l, r) in enumerate(queries):
            i, j = right[l], left[r] #get nearest candles for each query
            if i >= 0 and j >= 0 and i < j:
                ans[k] = presum[j] - presum[i + 1] #calculate plates between
        return ans

The Java, C++, and Go code follow a very similar structure and logic to the Python code, differing only in syntax and data structure implementations. The core idea of prefix sum and pre-computed arrays for efficient query processing remains the same across all languages.