{x}
blog image

Spiral Matrix IV

You are given two integers m and n, which represent the dimensions of a matrix.

You are also given the head of a linked list of integers.

Generate an m x n matrix that contains the integers in the linked list presented in spiral order (clockwise), starting from the top-left of the matrix. If there are remaining empty spaces, fill them with -1.

Return the generated matrix.

 

Example 1:

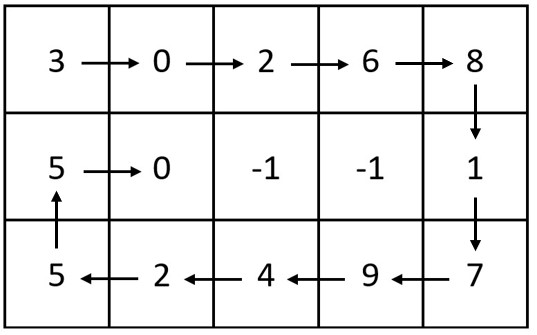
Input: m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0]
Output: [[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]]
Explanation: The diagram above shows how the values are printed in the matrix.
Note that the remaining spaces in the matrix are filled with -1.

Example 2:

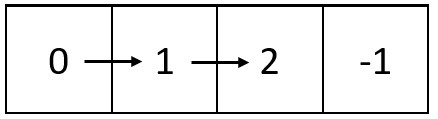
Input: m = 1, n = 4, head = [0,1,2]
Output: [[0,1,2,-1]]
Explanation: The diagram above shows how the values are printed from left to right in the matrix.
The last space in the matrix is set to -1.

 

Constraints:

  • 1 <= m, n <= 105
  • 1 <= m * n <= 105
  • The number of nodes in the list is in the range [1, m * n].
  • 0 <= Node.val <= 1000

Solution Explanation for Spiral Matrix IV

This problem involves creating an m x n matrix populated with values from a linked list in a spiral pattern (clockwise), filling remaining spaces with -1.

Approach: Simulation

The most straightforward approach is to simulate the spiral traversal. We use a matrix initialized with -1s and iterate through the linked list, placing each node's value into the matrix according to the spiral order.

Algorithm:

  1. Initialization:

    • Create an m x n matrix ans filled with -1.
    • Initialize i, j (row and column indices) to 0.
    • Initialize k (direction) to 0 (representing right). We'll use a dirs array to manage direction changes: dirs = [0, 1, 0, -1, 0] representing right, down, left, up.

  2. Spiral Traversal:

    • While the linked list head is not null (we still have values):
      • Place head.val into ans[i][j].
      • Move head to head.next.
      • Find Next Position:
        • Use a while loop to find the next valid position:
          • Calculate the next position (x, y) using i + dirs[k] and j + dirs[k+1].
          • If (x, y) is within the matrix bounds (0 <= x < m and 0 <= y < n) and ans[x][y] is -1 (unoccupied), update i and j to x and y respectively, and break the inner loop.
          • Otherwise, change direction by updating k = (k + 1) % 4.

  3. Return: Return the ans matrix.

Time and Space Complexity

  • Time Complexity: O(m * n) - In the worst case, we visit each cell of the matrix once. The linked list traversal is also linear in the number of nodes (which is at most m * n).
  • Space Complexity: O(m * n) - The matrix ans dominates the space complexity.

Code Implementation (Python)

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
 
class Solution:
    def spiralMatrix(self, m: int, n: int, head: Optional[ListNode]) -> List[List[int]]:
        ans = [[-1] * n for _ in range(m)]
        i = j = k = 0
        dirs = [0, 1, 0, -1, 0]  # Right, Down, Left, Up
 
        while head:
            ans[i][j] = head.val
            head = head.next
            while True:
                x, y = i + dirs[k], j + dirs[k + 1]
                if 0 <= x < m and 0 <= y < n and ans[x][y] == -1:
                    i, j = x, y
                    break
                k = (k + 1) % 4
        return ans

The implementations in Java, C++, Go, and TypeScript follow the same logic, differing only in syntax. The core algorithm remains consistent across all languages.