{x}
blog image

Number of Increasing Paths in a Grid

You are given an m x n integer matrix grid, where you can move from a cell to any adjacent cell in all 4 directions.

Return the number of strictly increasing paths in the grid such that you can start from any cell and end at any cell. Since the answer may be very large, return it modulo 109 + 7.

Two paths are considered different if they do not have exactly the same sequence of visited cells.

 

Example 1:

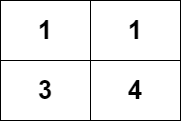
Input: grid = [[1,1],[3,4]]
Output: 8
Explanation: The strictly increasing paths are:
- Paths with length 1: [1], [1], [3], [4].
- Paths with length 2: [1 -> 3], [1 -> 4], [3 -> 4].
- Paths with length 3: [1 -> 3 -> 4].
The total number of paths is 4 + 3 + 1 = 8.

Example 2:

Input: grid = [[1],[2]]
Output: 3
Explanation: The strictly increasing paths are:
- Paths with length 1: [1], [2].
- Paths with length 2: [1 -> 2].
The total number of paths is 2 + 1 = 3.

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 1000
  • 1 <= m * n <= 105
  • 1 <= grid[i][j] <= 105

2328. Number of Increasing Paths in a Grid

Problem Description

Given an m x n integer matrix grid, you can move from a cell to any adjacent cell in all 4 directions. The task is to find the number of strictly increasing paths in the grid, starting and ending at any cell. The answer might be very large, so it should be returned modulo 10<sup>9</sup> + 7.

Solution: Depth-First Search (DFS) with Memoization

The most efficient approach is to use Depth-First Search (DFS) with memoization. This avoids redundant calculations by storing the results of subproblems.

Algorithm:

  1. dfs(i, j) function: This recursive function counts the number of strictly increasing paths starting from cell (i, j).
  2. Memoization: A 2D array f stores the results of dfs(i, j). If f[i][j] is non-zero, it means the result has already been computed, and we return the stored value.
  3. Base Case: If f[i][j] is 0 (not computed yet), we initialize f[i][j] to 1 (representing the path starting and ending at the current cell).
  4. Recursive Step: We explore the four adjacent cells. If an adjacent cell (x, y) has a value greater than the current cell's value (grid[i][j] < grid[x][y]), we recursively call dfs(x, y) and add the result to f[i][j].
  5. Modulo Operation: We use the modulo operator (% mod) to prevent integer overflow.
  6. Main Function: We iterate through each cell in the grid, calling dfs(i, j) for each cell and summing the results. This sum represents the total number of strictly increasing paths.

Time and Space Complexity Analysis

  • Time Complexity: O(m*n). In the worst case, we visit each cell once. The dfs function might recursively call itself multiple times, but due to memoization, each cell is visited at most once.
  • Space Complexity: O(m*n). This is due to the memoization array f which stores the results for each cell. The recursion depth is at most min(m, n).

Code Implementation (Python)

class Solution:
    def countPaths(self, grid: List[List[int]]) -> int:
        mod = 10**9 + 7
        m, n = len(grid), len(grid[0])
        f = [[0] * n for _ in range(m)]  # Memoization array
 
        def dfs(i, j):
            if f[i][j]:
                return f[i][j]
            f[i][j] = 1  # Initialize with 1 (path starting and ending at the cell)
            for dx, dy in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
                x, y = i + dx, j + dy
                if 0 <= x < m and 0 <= y < n and grid[x][y] > grid[i][j]:
                    f[i][j] = (f[i][j] + dfs(x, y)) % mod
            return f[i][j]
 
        total_paths = 0
        for i in range(m):
            for j in range(n):
                total_paths = (total_paths + dfs(i, j)) % mod
        return total_paths

Other Languages: The code can be easily adapted to other languages like Java, C++, JavaScript, etc., following the same algorithmic structure. The key elements are the dfs function with memoization and the modulo operation to handle large numbers.