{x}
blog image

Evaluate Boolean Binary Tree

You are given the root of a full binary tree with the following properties:

  • Leaf nodes have either the value 0 or 1, where 0 represents False and 1 represents True.
  • Non-leaf nodes have either the value 2 or 3, where 2 represents the boolean OR and 3 represents the boolean AND.

The evaluation of a node is as follows:

  • If the node is a leaf node, the evaluation is the value of the node, i.e. True or False.
  • Otherwise, evaluate the node's two children and apply the boolean operation of its value with the children's evaluations.

Return the boolean result of evaluating the root node.

A full binary tree is a binary tree where each node has either 0 or 2 children.

A leaf node is a node that has zero children.

 

Example 1:

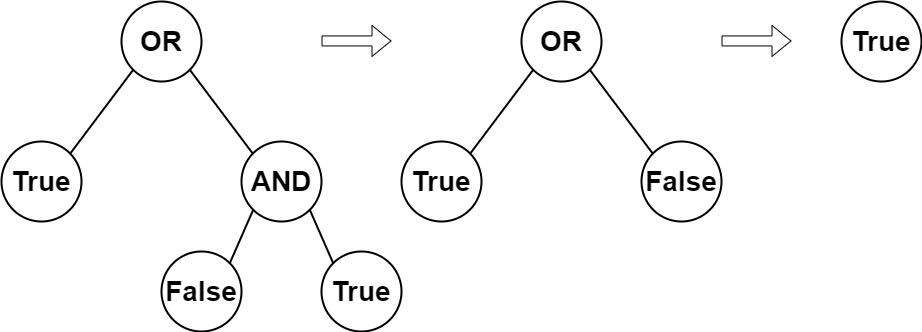
Input: root = [2,1,3,null,null,0,1]
Output: true
Explanation: The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.

Example 2:

Input: root = [0]
Output: false
Explanation: The root node is a leaf node and it evaluates to false, so we return false.

 

Constraints:

  • The number of nodes in the tree is in the range [1, 1000].
  • 0 <= Node.val <= 3
  • Every node has either 0 or 2 children.
  • Leaf nodes have a value of 0 or 1.
  • Non-leaf nodes have a value of 2 or 3.

2331. Evaluate Boolean Binary Tree

Problem Description

Given the root of a full binary tree where leaf nodes have values 0 or 1 (representing False or True), and non-leaf nodes have values 2 or 3 (representing OR and AND operations respectively), evaluate the tree and return the boolean result at the root.

Solution: Recursion

This problem is naturally solved using recursion. The recursive function evaluates a node based on its value:

  1. Base Case: If the node is a leaf (no left child), it directly returns True (if value is 1) or False (if value is 0).
  2. Recursive Step: If the node is not a leaf, it recursively evaluates its left and right children. Then:
    • If the node's value is 2 (OR), it returns the logical OR of the children's results.
    • If the node's value is 3 (AND), it returns the logical AND of the children's results.

Time and Space Complexity

  • Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited exactly once.
  • Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack. In the worst case (a skewed tree), H could be N, but for a balanced tree, H would be log₂(N).

Code Implementation (Python)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def evaluateTree(self, root: Optional[TreeNode]) -> bool:
        if root.left is None:  # Base case: leaf node
            return bool(root.val)
        
        left_result = self.evaluateTree(root.left)
        right_result = self.evaluateTree(root.right)
        
        if root.val == 2:  # OR operation
            return left_result or right_result
        else:  # AND operation
            return left_result and right_result

Code Implementation (Java)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean evaluateTree(TreeNode root) {
        if (root.left == null) { // Base case: leaf node
            return root.val == 1;
        }
 
        boolean leftResult = evaluateTree(root.left);
        boolean rightResult = evaluateTree(root.right);
 
        if (root.val == 2) { // OR operation
            return leftResult || rightResult;
        } else { // AND operation
            return leftResult && rightResult;
        }
    }
}

(Other language implementations (C++, Go, TypeScript, Rust, C) are similar in structure and logic, differing primarily in syntax.)

This recursive approach clearly reflects the problem's structure and is easy to understand and implement. The time and space complexities are acceptable for the given constraints.