- {x}
- Selling Pieces of Wood
- Minimum Flips in Binary Tree to Get Result
- The First Day of the Maximum Recorded Degree in Each City
- Count Asterisks
- Count Unreachable Pairs of Nodes in an Undirected Graph
- Maximum XOR After Operations
- Number of Distinct Roll Sequences
- Check if Matrix Is X-Matrix
- Count Number of Ways to Place Houses
- Maximum Score Of Spliced Array
- Minimum Score After Removals on a Tree
- Find Minimum Time to Finish All Jobs II
- Product Sales Analysis IV
- Decode the Message
- Spiral Matrix IV
- Number of People Aware of a Secret
- Number of Increasing Paths in a Grid
- Read More...

Count Number of Ways to Place Houses
There is a street with n * 2 plots, where there are n plots on each side of the street. The plots on each side are numbered from 1 to n. On each plot, a house can be placed.
Return the number of ways houses can be placed such that no two houses are adjacent to each other on the same side of the street. Since the answer may be very large, return it modulo 109 + 7.
Note that if a house is placed on the ith plot on one side of the street, a house can also be placed on the ith plot on the other side of the street.
Example 1:
Input: n = 1 Output: 4 Explanation: Possible arrangements: 1. All plots are empty. 2. A house is placed on one side of the street. 3. A house is placed on the other side of the street. 4. Two houses are placed, one on each side of the street.
Example 2:
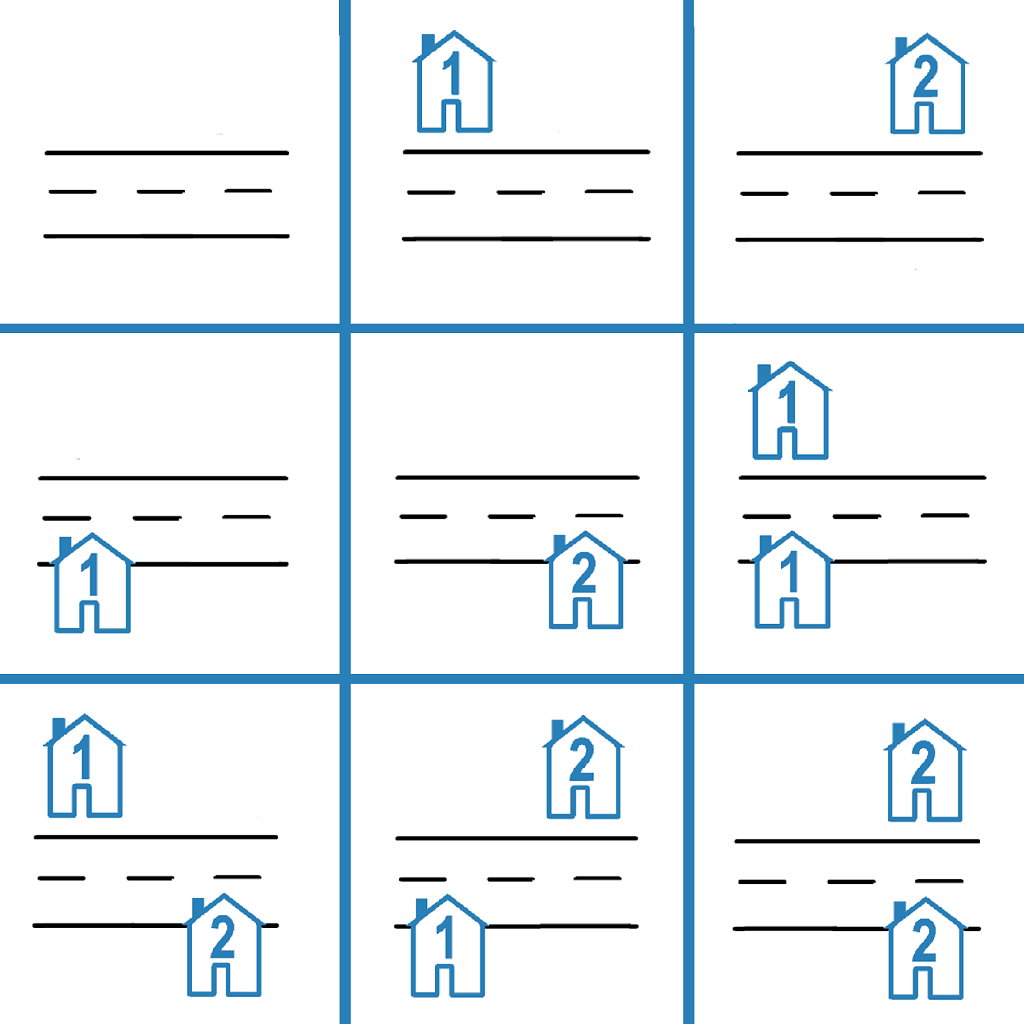
Input: n = 2 Output: 9 Explanation: The 9 possible arrangements are shown in the diagram above.
Constraints:
1 <= n <= 104
Solution Explanation
This problem asks to find the number of ways to place houses on two sides of a street with n plots on each side, such that no two houses are adjacent. The solution uses dynamic programming to efficiently calculate this count.
Approach
The core idea is to break down the problem into smaller subproblems. For each side of the street, we can define two recursive relations:
f(i): The number of ways to place houses on the firstiplots such that thei-th plot is not occupied by a house.g(i): The number of ways to place houses on the firstiplots such that thei-th plot is occupied by a house.
These relations can be expressed recursively:
f(i) = g(i-1)(If thei-th plot is empty, the(i-1)-th plot could be occupied or empty, henceg(i-1))g(i) = f(i-1) + g(i-1)(If thei-th plot is occupied, the(i-1)-th plot must be empty, givingf(i-1)ways; or it could be empty, givingg(i-1)ways).
The base cases are f(0) = 1 (no plots, one way: no houses) and g(0) = 1 (no plots, one way: no houses). g(1) would be 1, and f(1) would be 1 as well. We can see the patter here.
After calculating f(n) and g(n) for one side, the total number of ways for one side is f(n) + g(n). Since the two sides are independent, the total number of ways for both sides is (f(n) + g(n)) * (f(n) + g(n)).
Time and Space Complexity Analysis
- Time Complexity: O(n). The dynamic programming approach iterates through the
nplots once to calculatef(n)andg(n). - Space Complexity: O(n). The arrays
fandgstorenvalues each. This could be optimized to O(1) by using only the last two values.
Code Explanation (Python)
The Python code implements the dynamic programming approach:
class Solution:
def countHousePlacements(self, n: int) -> int:
mod = 10**9 + 7
f = [1] * n # Initialize f array
g = [1] * n # Initialize g array
for i in range(1, n):
f[i] = g[i - 1] # f(i) = g(i-1)
g[i] = (f[i - 1] + g[i - 1]) % mod # g(i) = (f(i-1) + g(i-1)) % mod
v = (f[-1] + g[-1]) % mod # Total ways for one side
return (v * v) % mod # Total ways for both sidesThe code initializes two arrays, f and g, with base cases. Then, it iteratively calculates f(i) and g(i) for i from 1 to n-1. Finally, it computes the total number of ways and returns the result modulo 10^9 + 7 to handle potential integer overflow. Other languages follow a very similar pattern.