- {x}
- Longest Binary Subsequence Less Than or Equal to K
- Selling Pieces of Wood
- Minimum Flips in Binary Tree to Get Result
- The First Day of the Maximum Recorded Degree in Each City
- Count Asterisks
- Count Unreachable Pairs of Nodes in an Undirected Graph
- Maximum XOR After Operations
- Number of Distinct Roll Sequences
- Check if Matrix Is X-Matrix
- Count Number of Ways to Place Houses
- Maximum Score Of Spliced Array
- Minimum Score After Removals on a Tree
- Find Minimum Time to Finish All Jobs II
- Product Sales Analysis IV
- Decode the Message
- Spiral Matrix IV
- Number of People Aware of a Secret
- Read More...

Check if Matrix Is X-Matrix
A square matrix is said to be an X-Matrix if both of the following conditions hold:
- All the elements in the diagonals of the matrix are non-zero.
- All other elements are 0.
Given a 2D integer array grid of size n x n representing a square matrix, return true if grid is an X-Matrix. Otherwise, return false.
Example 1:
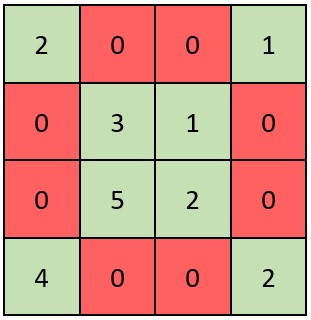
Input: grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]] Output: true Explanation: Refer to the diagram above. An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0. Thus, grid is an X-Matrix.
Example 2:
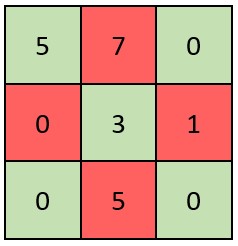
Input: grid = [[5,7,0],[0,3,1],[0,5,0]] Output: false Explanation: Refer to the diagram above. An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0. Thus, grid is not an X-Matrix.
Constraints:
n == grid.length == grid[i].length3 <= n <= 1000 <= grid[i][j] <= 105
Solution Explanation
The problem asks to determine if a given square matrix is an X-Matrix. An X-Matrix satisfies two conditions:
- All elements on the main diagonal and the anti-diagonal are non-zero.
- All other elements are zero.
The solution iterates through each element of the matrix and checks if it satisfies these conditions. If any element violates the conditions, the function immediately returns false. If the loop completes without finding any violations, it means the matrix is an X-Matrix, and the function returns true.
Time Complexity Analysis
The solution involves a single nested loop that iterates through all the elements of the n x n matrix. Therefore, the time complexity is O(n²). The operations inside the loop (comparisons and conditional checks) take constant time, O(1).
Space Complexity Analysis
The solution uses only a few variables to store indices and values, regardless of the input size. Thus, the space complexity is O(1), which is constant space.
Code Explanation (Python Example)
The Python code provided implements this strategy effectively:
class Solution:
def checkXMatrix(self, grid: List[List[int]]) -> bool:
for i, row in enumerate(grid):
for j, v in enumerate(row):
if i == j or i + j == len(grid) - 1: # Check if on diagonal
if v == 0: # Check for non-zero value
return False
elif v: # Check if off-diagonal element is non-zero
return False
return True- Outer Loop: The outer
forloop iterates through each row of the matrix usingenumerateto get both the index (i) and the row itself (row). - Inner Loop: The inner
forloop iterates through each element (v) in the current row usingenumerateto get the column index (j). - Diagonal Check:
if i == j or i + j == len(grid) - 1:checks if the current element is on either the main diagonal (i == j) or the anti-diagonal (i + j == len(grid) - 1). - Non-zero Check:
if v == 0:verifies that diagonal elements are non-zero. If a zero is found on a diagonal, it immediately returnsFalse. - Off-diagonal Check:
elif v:checks if any off-diagonal element is non-zero. If a non-zero element is found off the diagonals, it immediately returnsFalse. - Return True: If the loops complete without finding any violations, it means the matrix satisfies the conditions for an X-Matrix, and the function returns
True.
The other language examples follow a similar structure, differing only in syntax. They all maintain the same O(n²) time and O(1) space complexity.