{x}
blog image

Nearest Exit from Entrance in Maze

You are given an m x n matrix maze (0-indexed) with empty cells (represented as '.') and walls (represented as '+'). You are also given the entrance of the maze, where entrance = [entrancerow, entrancecol] denotes the row and column of the cell you are initially standing at.

In one step, you can move one cell up, down, left, or right. You cannot step into a cell with a wall, and you cannot step outside the maze. Your goal is to find the nearest exit from the entrance. An exit is defined as an empty cell that is at the border of the maze. The entrance does not count as an exit.

Return the number of steps in the shortest path from the entrance to the nearest exit, or -1 if no such path exists.

 

Example 1:

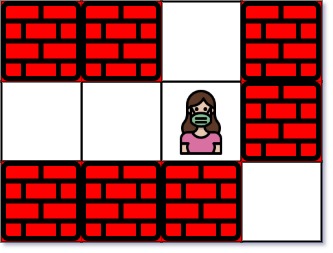
Input: maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
Output: 1
Explanation: There are 3 exits in this maze at [1,0], [0,2], and [2,3].
Initially, you are at the entrance cell [1,2].
- You can reach [1,0] by moving 2 steps left.
- You can reach [0,2] by moving 1 step up.
It is impossible to reach [2,3] from the entrance.
Thus, the nearest exit is [0,2], which is 1 step away.

Example 2:

Input: maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0]
Output: 2
Explanation: There is 1 exit in this maze at [1,2].
[1,0] does not count as an exit since it is the entrance cell.
Initially, you are at the entrance cell [1,0].
- You can reach [1,2] by moving 2 steps right.
Thus, the nearest exit is [1,2], which is 2 steps away.

Example 3:

Input: maze = [[".","+"]], entrance = [0,0]
Output: -1
Explanation: There are no exits in this maze.

 

Constraints:

  • maze.length == m
  • maze[i].length == n
  • 1 <= m, n <= 100
  • maze[i][j] is either '.' or '+'.
  • entrance.length == 2
  • 0 <= entrancerow < m
  • 0 <= entrancecol < n
  • entrance will always be an empty cell.

Solution Explanation: Nearest Exit from Entrance in Maze

This problem asks to find the shortest path from an entrance cell to any exit cell in a maze. An exit is defined as an empty cell on the border of the maze. The most efficient approach is using Breadth-First Search (BFS).

Approach:

BFS is ideal for finding the shortest path in an unweighted graph (like our maze). We treat empty cells as nodes and movements between adjacent empty cells as edges.

  1. Initialization:

    • Start with a queue q containing the entrance coordinates and its distance (0).
    • Mark the entrance cell as visited (e.g., by changing its value in the maze array to '+').

  2. BFS Iteration:

    • While the queue is not empty:
      • Dequeue the current cell (row, col, distance).
      • Explore its four neighboring cells (up, down, left, right).
      • For each neighbor:
        • Check if it's within the maze boundaries.
        • Check if it's an empty cell ('.'), and not already visited ('+').
        • If it's an exit cell (on the maze border), return distance + 1.
        • Otherwise, mark the neighbor as visited ('+'), enqueue it with distance + 1, indicating its distance from the entrance.

  3. No Exit Found:

    • If the queue becomes empty without finding an exit, return -1.

Time Complexity Analysis:

  • In the worst case, BFS visits every cell in the maze.
  • The number of cells is m * n, where m is the number of rows and n is the number of columns.
  • Therefore, the time complexity is O(m * n).

Space Complexity Analysis:

  • The space used is dominated by the queue.
  • In the worst-case scenario, the queue could hold all the cells in the maze.
  • Therefore, the space complexity is O(m * n).

Code Examples:

The code examples below implement the BFS approach in several programming languages. Note the slight variations in how the queue is managed and visited cells are marked. The core logic remains the same.

Python3:

from collections import deque
 
class Solution:
    def nearestExit(self, maze: List[List[str]], entrance: List[int]) -> int:
        m, n = len(maze), len(maze[0])
        q = deque([(entrance[0], entrance[1], 0)])  # (row, col, distance)
        maze[entrance[0]][entrance[1]] = '+'  # Mark entrance as visited
 
        while q:
            row, col, dist = q.popleft()
            for dr, dc in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
                new_row, new_col = row + dr, col + dc
                if 0 <= new_row < m and 0 <= new_col < n:
                    if maze[new_row][new_col] == '.':
                        if new_row == 0 or new_row == m - 1 or new_col == 0 or new_col == n - 1:
                            return dist + 1
                        maze[new_row][new_col] = '+'
                        q.append((new_row, new_col, dist + 1))
        return -1

Java:

import java.util.*;
 
class Solution {
    public int nearestExit(char[][] maze, int[] entrance) {
        int m = maze.length, n = maze[0].length;
        Queue<int[]> q = new LinkedList<>();
        q.offer(new int[] {entrance[0], entrance[1], 0}); // {row, col, dist}
        maze[entrance[0]][entrance[1]] = '+';
 
        while (!q.isEmpty()) {
            int[] curr = q.poll();
            int row = curr[0], col = curr[1], dist = curr[2];
            for (int[] dr : new int[][] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}) {
                int new_row = row + dr[0], new_col = col + dr[1];
                if (new_row >= 0 && new_row < m && new_col >= 0 && new_col < n) {
                    if (maze[new_row][new_col] == '.') {
                        if (new_row == 0 || new_row == m - 1 || new_col == 0 || new_col == n - 1)
                            return dist + 1;
                        maze[new_row][new_col] = '+';
                        q.offer(new int[] {new_row, new_col, dist + 1});
                    }
                }
            }
        }
        return -1;
    }
}

(Other languages like C++, Go, TypeScript would follow a similar structure, adapting syntax and data structures accordingly.)