{x}
blog image

Number of Ways of Cutting a Pizza

Given a rectangular pizza represented as a rows x cols matrix containing the following characters: 'A' (an apple) and '.' (empty cell) and given the integer k. You have to cut the pizza into k pieces using k-1 cuts. 

For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.

Return the number of ways of cutting the pizza such that each piece contains at least one apple. Since the answer can be a huge number, return this modulo 10^9 + 7.

 

Example 1:

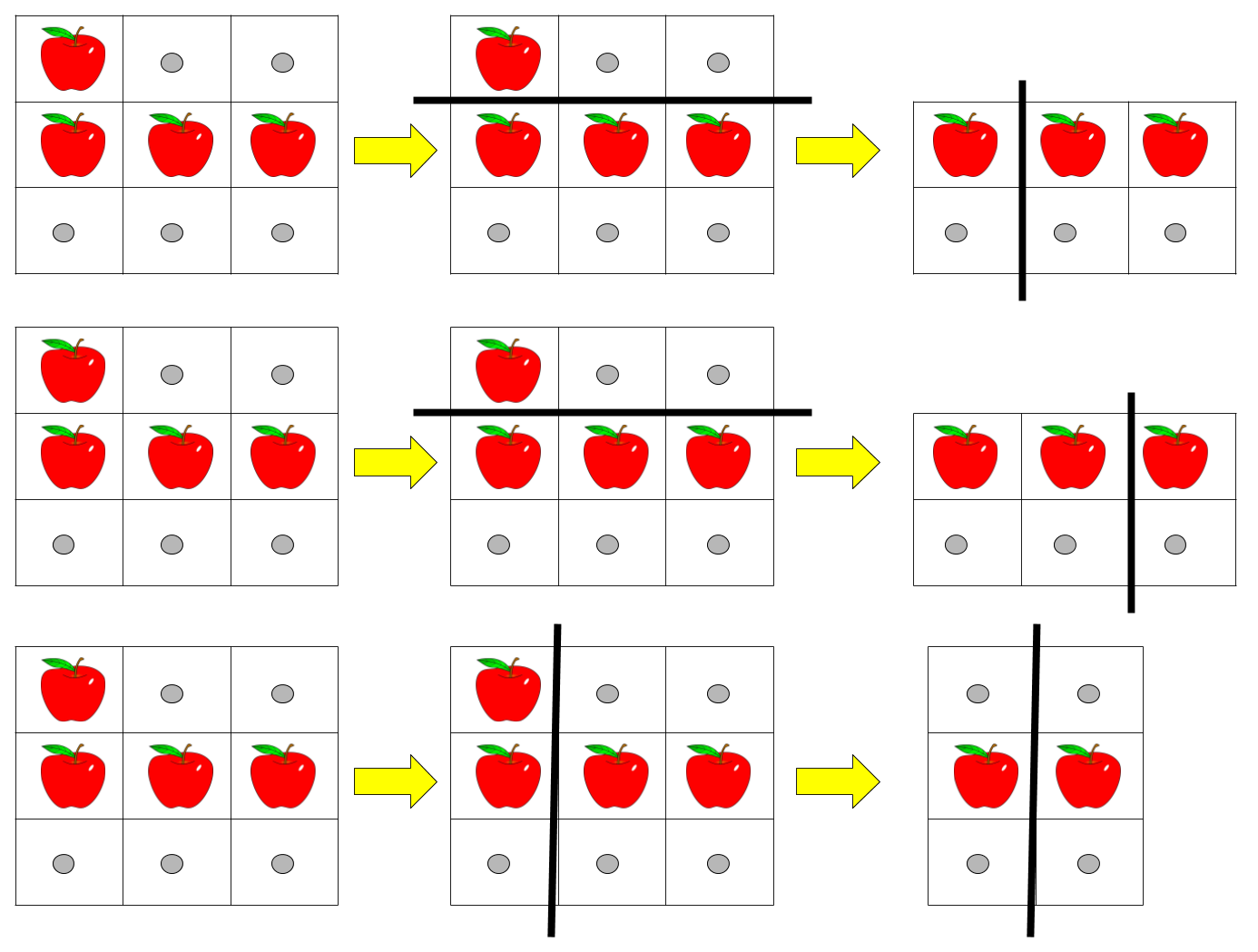
Input: pizza = ["A..","AAA","..."], k = 3
Output: 3 
Explanation: The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.

Example 2:

Input: pizza = ["A..","AA.","..."], k = 3
Output: 1

Example 3:

Input: pizza = ["A..","A..","..."], k = 1
Output: 1

 

Constraints:

  • 1 <= rows, cols <= 50
  • rows == pizza.length
  • cols == pizza[i].length
  • 1 <= k <= 10
  • pizza consists of characters 'A' and '.' only.

1444. Number of Ways of Cutting a Pizza

This problem asks to find the number of ways to cut a pizza into k pieces such that each piece contains at least one apple. The pizza is represented as a matrix of 'A' (apple) and '.' (empty). Cuts can be horizontal or vertical.

Approach: 2D Prefix Sum + Memoized DFS

The solution uses a dynamic programming approach with memoization to efficiently explore the search space. Here's a breakdown:

  1. 2D Prefix Sum: A crucial optimization is pre-computing a 2D prefix sum array s. s[i][j] stores the total number of apples in the sub-rectangle from (0, 0) to (i, j). This allows for O(1) computation of the number of apples in any sub-rectangle.

  2. Memoized Depth-First Search (DFS): The core logic is a recursive DFS function dfs(i, j, k):

    • i, j: Top-left coordinates of the current pizza piece being considered.
    • k: The number of cuts remaining.

    The base cases are:

    • k == 0: No more cuts needed. Check if the current piece has at least one apple (s[m][n] - s[i][n] - s[m][j] + s[i][j] > 0). If yes, return 1 (one way); otherwise, return 0.
    • Memoization: If dfs(i, j, k) has already been computed, return the stored value.

    The recursive step explores two possibilities for each cut:

    • Horizontal Cut: Iterate through possible horizontal cut positions x (i < x < m). Check if the top piece (0,0 to x,n) contains at least one apple. If so, recursively call dfs(x, j, k - 1) for the bottom piece and add the result to the count.
    • Vertical Cut: Iterate through possible vertical cut positions y (j < y < n). Check if the left piece (0,0 to m,y) contains at least one apple. If so, recursively call dfs(i, y, k - 1) for the right piece and add the result to the count.

  3. Result: The final answer is dfs(0, 0, k - 1), representing the number of ways to cut the entire pizza into k pieces with k-1 cuts. The modulo operation (% mod) is used to handle potential large numbers.

Time and Space Complexity

  • Time Complexity: O(m * n * k * (m + n)). The DFS explores all possible cut combinations. The prefix sum calculation is O(m * n).
  • Space Complexity: O(m * n * k). This is dominated by the memoization array f.

Code (Python)

class Solution:
    def ways(self, pizza: List[str], k: int) -> int:
        mod = 10**9 + 7
        m, n = len(pizza), len(pizza[0])
        s = [[0] * (n + 1) for _ in range(m + 1)]  # Prefix sum array
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + (pizza[i - 1][j - 1] == 'A')
 
        @cache
        def dfs(i, j, k):  # Memoized DFS
            if k == 0:
                return int(s[m][n] - s[i][n] - s[m][j] + s[i][j] > 0)
            ans = 0
            for x in range(i + 1, m):
                if s[x][n] - s[i][n] - s[x][j] + s[i][j] > 0:
                    ans = (ans + dfs(x, j, k - 1)) % mod
            for y in range(j + 1, n):
                if s[m][y] - s[i][y] - s[m][j] + s[i][j] > 0:
                    ans = (ans + dfs(i, y, k - 1)) % mod
            return ans
 
        return dfs(0, 0, k - 1)

The code in other languages (Java, C++, Go, TypeScript) follows a very similar structure, differing only in syntax and data structure implementations. The core algorithm remains the same.