- {x}
- First Unique Number
- Check If a String Is a Valid Sequence from Root to Leaves Path in a Binary Tree
- Kids With the Greatest Number of Candies
- Max Difference You Can Get From Changing an Integer
- Check If a String Can Break Another String
- Number of Ways to Wear Different Hats to Each Other
- Create a Session Bar Chart
- Destination City
- Check If All 1's Are at Least Length K Places Away
- Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit
- Find the Kth Smallest Sum of a Matrix With Sorted Rows
- Evaluate Boolean Expression
- Build an Array With Stack Operations
- Count Triplets That Can Form Two Arrays of Equal XOR
- Minimum Time to Collect All Apples in a Tree
- Number of Ways of Cutting a Pizza
- Apples & Oranges
- Read More...

Check If All 1's Are at Least Length K Places Away
Given an binary array nums and an integer k, return true if all 1's are at least k places away from each other, otherwise return false.
Example 1:
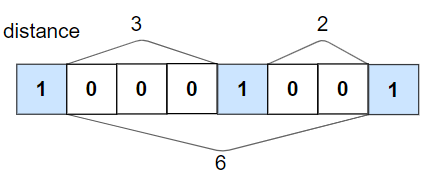
Input: nums = [1,0,0,0,1,0,0,1], k = 2 Output: true Explanation: Each of the 1s are at least 2 places away from each other.
Example 2:
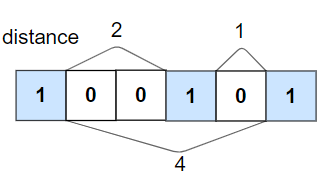
Input: nums = [1,0,0,1,0,1], k = 2 Output: false Explanation: The second 1 and third 1 are only one apart from each other.
Constraints:
1 <= nums.length <= 1050 <= k <= nums.lengthnums[i]is0or1
Solution Explanation
This problem asks whether all occurrences of the digit 1 in a binary array are separated by at least k zeros. The solution uses a single pass through the array to efficiently determine this.
Approach:
The core idea is to track the index j of the last encountered 1. For each element, we check:
-
Is it a 1? If so, we calculate the distance between the current index
iand the previously seen 1's indexj. If this distance (minus 1 to exclude the 1s themselves) is less thank, it means the 1s are too close, and we returnfalse. Otherwise, we updatejto the current indexi. -
Is it a 0? If it's a 0, we simply continue iterating.
If the loop completes without finding any 1s that are too close, we return true.
Time Complexity Analysis:
The solution iterates through the input array nums exactly once. Therefore, the time complexity is O(n), where n is the length of the array.
Space Complexity Analysis:
The solution uses a constant amount of extra space to store the variables i, j, and k. Therefore, the space complexity is O(1), which is constant space.
Code Explanation (Python):
class Solution:
def kLengthApart(self, nums: List[int], k: int) -> bool:
j = -float('inf') # Initialize j to negative infinity. This handles the case of the first 1.
for i, x in enumerate(nums):
if x: #if x ==1
if i - j - 1 < k: #check if the distance between the current 1 and the previous 1 is less than k
return False #if yes return false
j = i #update j to current index if the distance is greater than k
return True #return true if all 1s are at least k places awayThe other languages (Java, C++, Go, TypeScript) follow the same logic, with minor syntactic variations. The key idea of tracking the last seen 1 and efficiently checking the distance remains consistent across all implementations.