{x}
blog image

Minimum Time to Collect All Apples in a Tree

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.

 

Example 1:

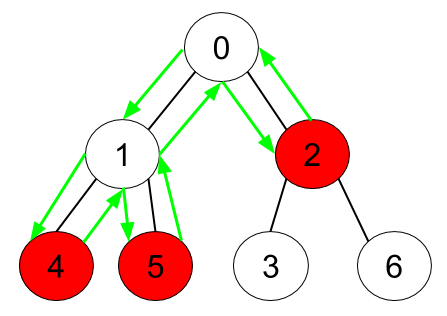
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.

Example 2:

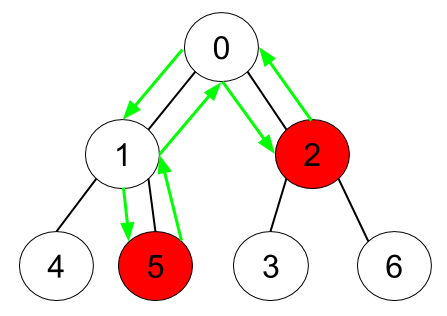
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

 

Constraints:

  • 1 <= n <= 105
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai < bi <= n - 1
  • hasApple.length == n

Solution Explanation

This problem can be efficiently solved using Depth-First Search (DFS). The goal is to find the minimum time to collect all apples, starting and ending at node 0.

Approach:

The DFS approach traverses the tree, recursively exploring each branch. The key insight is that we only need to traverse edges leading to nodes with apples or nodes that lead to apples further down the tree. If a subtree contains no apples, we don't need to visit it.

The function dfs performs the following steps:

  1. Base Case: If a node u has already been visited (vis[u]), it returns 0 (no additional time is needed).

  2. Mark as Visited: The current node u is marked as visited (vis[u] = True).

  3. Recursive Calls: It recursively calls dfs for each neighbor (v) of node u. The cost of traversing each edge is 2 (going to a neighbor and coming back). The total cost from the recursive calls is accumulated in nxt_cost.

  4. Apple Check: If node u doesn't have an apple (!hasApple[u]) and there's no cost accumulated from its subtrees (nxt_cost == 0), it means this subtree is irrelevant, and we return 0.

  5. Return Value: If the node has an apple or its subtree contains apples, it returns cost + nxt_cost, where cost represents the cost of reaching the current node (2 for each edge).

The initial call to dfs(0, 0) starts the traversal from node 0 with an initial cost of 0.

Time and Space Complexity Analysis

Time Complexity: O(V + E), where V is the number of vertices (nodes) and E is the number of edges in the tree. This is because the DFS algorithm visits each node and edge at most once.

Space Complexity: O(V), where V is the number of vertices. This space is used primarily by the recursion stack during the depth-first search and the vis array to keep track of visited nodes. In the worst case (a long, thin tree), the recursion depth can be equal to the number of vertices.

Code Implementation (Python3)

from collections import defaultdict
 
class Solution:
    def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:
        def dfs(u, cost):
            if vis[u]:
                return 0
            vis[u] = True
            nxt_cost = 0
            for v in g[u]:
                nxt_cost += dfs(v, 2)
            if not hasApple[u] and nxt_cost == 0:
                return 0
            return cost + nxt_cost
 
        g = defaultdict(list)
        for u, v in edges:
            g[u].append(v)
            g[v].append(u)
        vis = [False] * n
        return dfs(0, 0)

The other languages (Java, C++, Go) follow a very similar structure, differing only in syntax. The core algorithm and complexity remain the same.