{x}
blog image

Minimum Cost to Make at Least One Valid Path in a Grid

Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:

  • 1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
  • 2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
  • 3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
  • 4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])

Notice that there could be some signs on the cells of the grid that point outside the grid.

You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

 

Example 1:

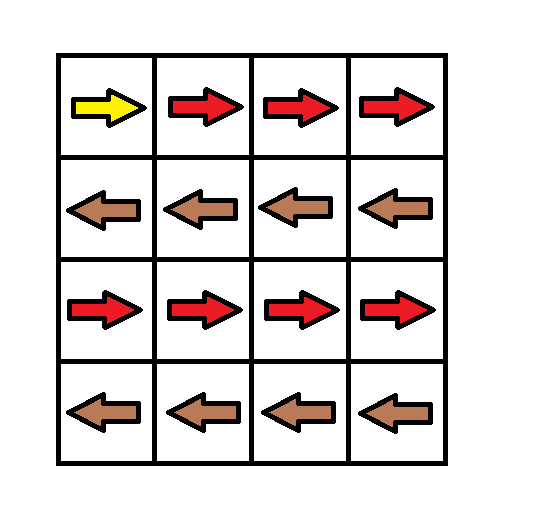
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:

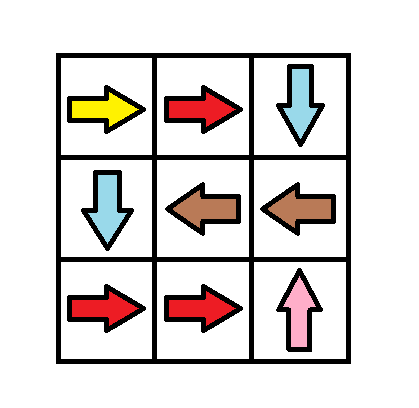
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:

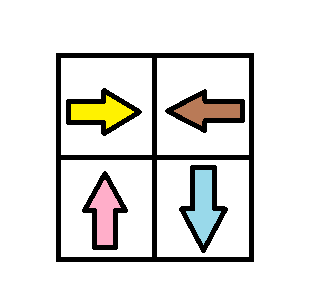
Input: grid = [[1,2],[4,3]]
Output: 1

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 100
  • 1 <= grid[i][j] <= 4

Solution Explanation: Minimum Cost to Make at Least One Valid Path in a Grid

This problem asks for the minimum cost to modify the directions in a grid to create at least one valid path from the top-left corner (0,0) to the bottom-right corner (m-1, n-1). The cost of changing a direction is 1.

Approach:

The optimal approach is using a variation of Breadth-First Search (BFS) with a deque (double-ended queue). A standard BFS wouldn't be efficient enough because it doesn't prioritize exploring paths that require fewer changes.

  1. Initialization:

    • We start at (0, 0) with a cost of 0.
    • We use a deque to store the cells to visit. The deque allows us to add elements to both ends, which is crucial for efficiency.
    • A visited set keeps track of cells we've already explored to avoid cycles.

  2. BFS with Deque:

    • The deque is prioritized. Cells reachable without changing direction (cost 0) are added to the front of the deque. Cells requiring a direction change (cost 1) are added to the back. This ensures that we explore paths with fewer direction changes first.
    • During each iteration, we:
      • Dequeue a cell (i, j) from the front of the deque.
      • If the cell is already visited, continue.
      • Mark the cell as visited.
      • If we reach the target cell (m-1, n-1), return the current cost d.
      • Explore all four possible directions (up, down, left, right) from (i, j):
        • If the direction matches the existing direction in the grid, add the neighboring cell to the front of the deque (cost 0).
        • If the direction does not match, add the neighboring cell to the back of the deque (cost 1, incrementing the cost d).

  3. Handling Out-of-Bounds: We need to check that the next cell is within the bounds of the grid before processing it.

  4. No Valid Path: If the deque becomes empty before reaching the target cell, it means there is no valid path, and we can return -1 (though the problem statement implies there will always be a solution).

Time Complexity: O(M*N), where M and N are the dimensions of the grid. In the worst case, we visit each cell once.

Space Complexity: O(M*N), in the worst case, we store all cells in the deque and visited set.

Code (Python):

from collections import deque
 
def minCost(grid):
    m, n = len(grid), len(grid[0])
    dirs = [(0, 1), (0, -1), (1, 0), (-1, 0)]  # Right, Left, Down, Up
    q = deque([(0, 0, 0)])  # (row, col, cost)
    visited = set()
    while q:
        row, col, cost = q.popleft()
        if (row, col) in visited:
            continue
        visited.add((row, col))
        if row == m - 1 and col == n - 1:
            return cost
        for i, (dr, dc) in enumerate(dirs):
            next_row, next_col = row + dr, col + dc
            if 0 <= next_row < m and 0 <= next_col < n:
                new_cost = cost + (i + 1 != grid[row][col]) #Increment cost if direction change is needed
                if (i+1) == grid[row][col]:
                    q.appendleft((next_row, next_col, new_cost))
                else:
                    q.append((next_row, next_col, new_cost))
    return -1  # Should not reach here based on problem statement

The code in other languages (Java, C++, Go, TypeScript) follows the same logic, using their respective deque implementations and data structures. The core algorithm remains consistent.