- {x}
- How Many Numbers Are Smaller Than the Current Number
- Rank Teams by Votes
- Linked List in Binary Tree
- Minimum Cost to Make at Least One Valid Path in a Grid
- Get the Second Most Recent Activity
- Increasing Decreasing String
- Find the Longest Substring Containing Vowels in Even Counts
- Longest ZigZag Path in a Binary Tree
- Maximum Sum BST in Binary Tree
- Generate a String With Characters That Have Odd Counts
- Number of Times Binary String Is Prefix-Aligned
- Time Needed to Inform All Employees
- Frog Position After T Seconds
- Replace Employee ID With The Unique Identifier
- Find a Corresponding Node of a Binary Tree in a Clone of That Tree
- Lucky Numbers in a Matrix
- Design a Stack With Increment Operation
- Read More...

Maximum Sum BST in Binary Tree
Given a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
Example 1:
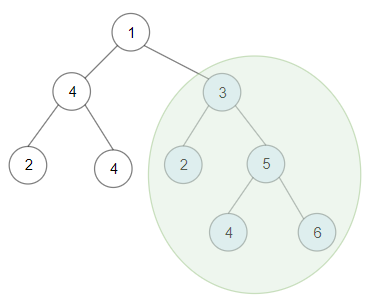
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6] Output: 20 Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.
Example 2:
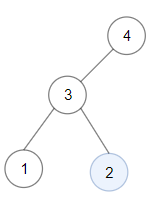
Input: root = [4,3,null,1,2] Output: 2 Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.
Example 3:
Input: root = [-4,-2,-5] Output: 0 Explanation: All values are negatives. Return an empty BST.
Constraints:
- The number of nodes in the tree is in the range
[1, 4 * 104]. -4 * 104 <= Node.val <= 4 * 104
Solution Explanation: Maximum Sum BST in Binary Tree
This problem asks to find the maximum sum of nodes within a subtree that also forms a valid Binary Search Tree (BST). A simple traversal isn't sufficient because we need to simultaneously check for BST properties and track the maximum sum. The optimal solution uses Depth-First Search (DFS) with a clever return value from the recursive function.
Approach: Post-Order DFS with Tuple Return Value
The core idea is to perform a post-order DFS traversal. For each node, we recursively explore the left and right subtrees. The key is what information we return from the recursive calls: a 4-element tuple. This tuple efficiently summarizes the results of the subtree exploration:
bst(boolean): Indicates whether the subtree rooted at the current node is a valid BST (true/false).min(integer): The minimum value in the subtree.max(integer): The maximum value in the subtree.sum(integer): The sum of all node values in the subtree.
The dfs function works as follows:
-
Base Case (Leaf Node or
null): If the current node is null (empty subtree), it's considered a valid BST with min = ∞, max = -∞, and sum = 0. -
Recursive Calls: Recursively calls
dfson the left and right subtrees, obtaining their respective tuples. -
BST Check and Update: A subtree rooted at the current node is a valid BST only if:
- Both the left and right subtrees are valid BSTs (
lbstandrbstare true). - The maximum value in the left subtree is strictly less than the current node's value (
lmx < root.val). - The minimum value in the right subtree is strictly greater than the current node's value (
root.val < rmi).
- Both the left and right subtrees are valid BSTs (
-
Sum Calculation: If the subtree is a valid BST, calculate its sum (
s = ls + rs + root.val). Update the global maximum sum (ans) if necessary. -
Return Value: Return a tuple containing (
bst,min,max,sum). Theminandmaxvalues are updated to reflect the minimum and maximum values of the current subtree.
Time and Space Complexity Analysis
- Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited exactly once during the DFS traversal.
- Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack in the DFS. In the worst case (a skewed tree), H could be N, resulting in O(N) space complexity.
Code Implementation (Python)
class Solution:
def maxSumBST(self, root: Optional[TreeNode]) -> int:
self.ans = 0
inf = float('inf') # Use float('inf') for infinity
def dfs(node):
if not node:
return True, inf, -inf, 0
lbst, lmin, lmax, lsum = dfs(node.left)
rbst, rmin, rmax, rsum = dfs(node.right)
if lbst and rbst and lmax < node.val < rmin:
bst = True
min_val = min(node.val, lmin)
max_val = max(node.val, rmax)
sum_val = lsum + rsum + node.val
self.ans = max(self.ans, sum_val)
return bst, min_val, max_val, sum_val
else:
return False, 0, 0, 0 #Invalid BST
dfs(root)
return self.ansThe code in other languages (Java, C++, Go, TypeScript) follows the same logic, just with syntax variations for handling tuples/arrays and infinity. The essential structure of the dfs function remains consistent across all languages.