{x}
blog image

Longest ZigZag Path in a Binary Tree

You are given the root of a binary tree.

A ZigZag path for a binary tree is defined as follow:

  • Choose any node in the binary tree and a direction (right or left).
  • If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
  • Change the direction from right to left or from left to right.
  • Repeat the second and third steps until you can't move in the tree.

Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).

Return the longest ZigZag path contained in that tree.

 

Example 1:

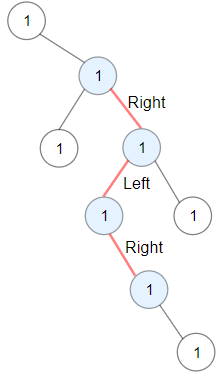
Input: root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1]
Output: 3
Explanation: Longest ZigZag path in blue nodes (right -> left -> right).

Example 2:

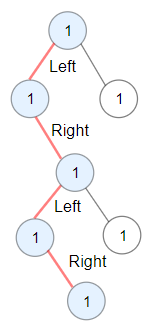
Input: root = [1,1,1,null,1,null,null,1,1,null,1]
Output: 4
Explanation: Longest ZigZag path in blue nodes (left -> right -> left -> right).

Example 3:

Input: root = [1]
Output: 0

 

Constraints:

  • The number of nodes in the tree is in the range [1, 5 * 104].
  • 1 <= Node.val <= 100

Solution Explanation

This problem asks for the longest ZigZag path in a binary tree. A ZigZag path is defined as a path where you alternate between moving left and right children. The solution uses Depth-First Search (DFS) with a recursive helper function to efficiently find this path.

Approach:

The core idea is to track the length of ZigZag paths from each node. Instead of explicitly checking for left-right or right-left movements, we cleverly use two parameters, l and r, to represent the length of ZigZag paths ending with a left move and a right move respectively.

  1. Base Case: If the current node (root) is null, the recursion stops, and nothing is done.

  2. Update Maximum Length: The maximum length encountered so far (ans) is updated with the maximum of l and r. This represents the longest ZigZag path found up to the current node.

  3. Recursive Calls: Two recursive calls are made:

    • dfs(root.left, r + 1, 0): If we move to the left child, we increment the r (right-ending path length) because the previous move was to the right, and the l (left-ending path length) is reset to 0.
    • dfs(root.right, 0, l + 1): If we move to the right child, we increment l (left-ending path length) as the previous move was to the left and r is reset.

Time Complexity: O(N), where N is the number of nodes in the tree. The DFS visits each node exactly once.

Space Complexity: O(H), where H is the height of the tree. This accounts for the recursive call stack space in the worst-case scenario of a skewed tree. In a balanced tree, this becomes O(log N).

Code Explanation (Python3 Example)

class Solution:
    def longestZigZag(self, root: TreeNode) -> int:
        def dfs(root, l, r):
            if root is None:
                return
            nonlocal ans
            ans = max(ans, l, r)
            dfs(root.left, r + 1, 0)
            dfs(root.right, 0, l + 1)
 
        ans = 0
        dfs(root, 0, 0)
        return ans
  • ans: A global variable to keep track of the maximum ZigZag path length.
  • dfs(root, l, r): The recursive helper function.
    • root: The current node being processed.
    • l: Length of the ZigZag path ending with a left move.
    • r: Length of the ZigZag path ending with a right move.
  • The nonlocal ans statement ensures that we are modifying the global ans variable, not creating a local copy.
  • The base case checks if the current node is None.
  • The recursive calls explore the left and right subtrees, updating l and r appropriately.

The other languages (Java, C++, Go) follow the same logic and algorithmic structure, merely differing in syntax. They all leverage a recursive DFS approach to efficiently compute the longest ZigZag path length.