{x}
blog image

Validate Binary Tree Nodes

You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

 

Example 1:

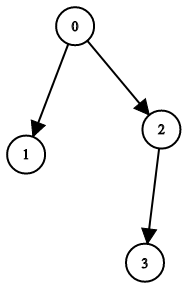
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

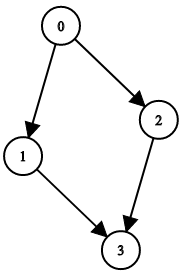
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

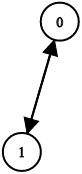
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

 

Constraints:

  • n == leftChild.length == rightChild.length
  • 1 <= n <= 104
  • -1 <= leftChild[i], rightChild[i] <= n - 1

Solution Explanation: Validate Binary Tree Nodes

This problem asks whether a given set of nodes and their parent-child relationships form a valid binary tree. A valid binary tree has exactly one root node (a node with no parent) and avoids cycles. This solution uses a Union-Find algorithm for efficient cycle detection and root identification.

Approach:

  1. Union-Find Data Structure: A Union-Find data structure is used to track connected components. Each node initially represents its own component. When a parent-child relationship is established, their components are merged using the union() operation (implemented as find() and setting p[find(i)] = find(j) in the code).

  2. Cycle Detection: Before merging components, the algorithm checks if a child node (j) already belongs to the same component as its parent node (i). If they're in the same component, it indicates a cycle (invalid tree), and false is returned. Similarly, it checks if the child already has a parent (vis[j]).

  3. Root Identification: A valid binary tree will have exactly one root node after all parent-child relationships are processed. The algorithm keeps track of the number of remaining components (n). After the loop, if n == 1, it means all nodes belong to the same component (one tree), implying a valid binary tree.

Time Complexity: O(Nα(N)), where N is the number of nodes and α(N) is the inverse Ackermann function, which is practically a constant (very small). Union-Find operations (find and union) take amortized O(α(N)) time.

Space Complexity: O(N) to store the parent array (p) and the visited array (vis).

Code Explanation (Python):

class Solution:
    def validateBinaryTreeNodes(
        self, n: int, leftChild: List[int], rightChild: List[int]
    ) -> bool:
        def find(x: int) -> int:  # Find the root of the component
            if p[x] != x:
                p[x] = find(p[x])  # Path compression for efficiency
            return p[x]
 
        p = list(range(n))  # Initialize parent array (each node is its own parent)
        vis = [False] * n  # Track visited nodes
        for i, (a, b) in enumerate(zip(leftChild, rightChild)): #Iterate through nodes and their children
            for j in (a, b): #Check both left and right children
                if j != -1:  #If child exists
                    if vis[j] or find(i) == find(j): #Cycle detection
                        return False
                    p[find(i)] = find(j)  #Union operation: merge components
                    vis[j] = True  #Mark child as visited
                    n -= 1 #Decrement the number of components
 
        return n == 1  #Check if only one component remains (a single tree)

The Java, C++, and Go code follow the same logic, differing only in syntax. The core Union-Find operations remain consistent across all implementations.