- {x}
- Mean of Array After Removing Some Elements
- Coordinate With Maximum Network Quality
- Number of Sets of K Non-Overlapping Line Segments
- Fancy Sequence
- All Valid Triplets That Can Represent a Country
- Largest Substring Between Two Equal Characters
- Lexicographically Smallest String After Applying Operations
- Best Team With No Conflicts
- Graph Connectivity With Threshold
- Design an Expression Tree With Evaluate Function
- Slowest Key
- Arithmetic Subarrays
- Path With Minimum Effort
- Rank Transform of a Matrix
- Percentage of Users Attended a Contest
- Add Two Polynomials Represented as Linked Lists
- Hopper Company Queries I
- Read More...

Graph Connectivity With Threshold
We have n cities labeled from 1 to n. Two different cities with labels x and y are directly connected by a bidirectional road if and only if x and y share a common divisor strictly greater than some threshold. More formally, cities with labels x and y have a road between them if there exists an integer z such that all of the following are true:
x % z == 0,y % z == 0, andz > threshold.
Given the two integers, n and threshold, and an array of queries, you must determine for each queries[i] = [ai, bi] if cities ai and bi are connected directly or indirectly. (i.e. there is some path between them).
Return an array answer, where answer.length == queries.length and answer[i] is true if for the ith query, there is a path between ai and bi, or answer[i] is false if there is no path.
Example 1:
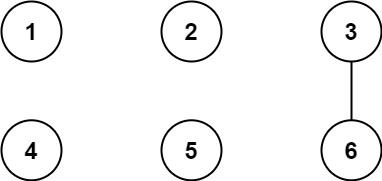
Input: n = 6, threshold = 2, queries = [[1,4],[2,5],[3,6]] Output: [false,false,true] Explanation: The divisors for each number: 1: 1 2: 1, 2 3: 1, 3 4: 1, 2, 4 5: 1, 5 6: 1, 2, 3, 6 Using the underlined divisors above the threshold, only cities 3 and 6 share a common divisor, so they are the only ones directly connected. The result of each query: [1,4] 1 is not connected to 4 [2,5] 2 is not connected to 5 [3,6] 3 is connected to 6 through path 3--6
Example 2:
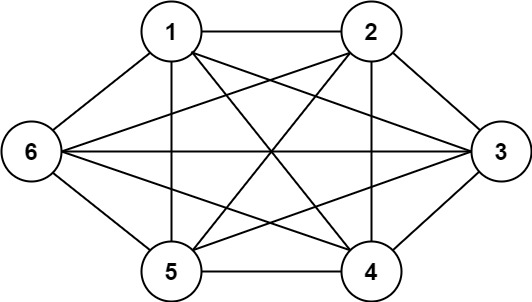
Input: n = 6, threshold = 0, queries = [[4,5],[3,4],[3,2],[2,6],[1,3]] Output: [true,true,true,true,true] Explanation: The divisors for each number are the same as the previous example. However, since the threshold is 0, all divisors can be used. Since all numbers share 1 as a divisor, all cities are connected.
Example 3:
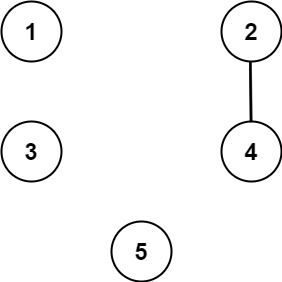
Input: n = 5, threshold = 1, queries = [[4,5],[4,5],[3,2],[2,3],[3,4]] Output: [false,false,false,false,false] Explanation: Only cities 2 and 4 share a common divisor 2 which is strictly greater than the threshold 1, so they are the only ones directly connected. Please notice that there can be multiple queries for the same pair of nodes [x, y], and that the query [x, y] is equivalent to the query [y, x].
Constraints:
2 <= n <= 1040 <= threshold <= n1 <= queries.length <= 105queries[i].length == 21 <= ai, bi <= citiesai != bi
Solution Explanation:
This problem asks to determine if two cities are connected either directly or indirectly given a threshold and a list of queries. Two cities are directly connected if they share a common divisor strictly greater than the threshold. The solution uses a Union-Find data structure to efficiently determine connectivity.
Approach:
-
Union-Find Data Structure: A Union-Find data structure is used to maintain disjoint sets of connected cities. Each city is initially in its own set. When two cities are found to be directly connected (sharing a common divisor greater than the threshold), their sets are merged using the
unionoperation. -
Finding Common Divisors: The algorithm iterates through possible divisors (
z) starting fromthreshold + 1. For each divisor, it finds all multiples of that divisor within the range of cities (1 to n). These multiples represent cities directly connected because they all sharezas a common divisor. Theunionoperation is then used to connect these cities in the Union-Find data structure. -
Query Processing: For each query
[a, b], the algorithm uses thefindoperation in the Union-Find structure. Iffind(a)equalsfind(b), then citiesaandbare in the same set, meaning they are connected (either directly or indirectly), and the result istrue. Otherwise, they are not connected, and the result isfalse.
Time Complexity Analysis:
- Initialization: Creating the Union-Find data structure takes O(n) time.
- Finding Common Divisors: The outer loop iterates up to n times (for each possible divisor). The inner loop iterates approximately n/a times for divisor a. Thus, the total time complexity for finding common divisors is approximately O(n log n) in the worst case. (The harmonic series sum is approximately O(n log n)).
- Union Operations: Each union operation takes almost constant time, O(α(n)), where α(n) is the inverse Ackermann function, which grows incredibly slowly and can be considered constant for all practical purposes. Since there are at most n union operations, this contributes O(n) to the time complexity.
- Query Processing: Each query takes O(α(n)) time for two
findoperations. Therefore, processing q queries takes O(q * α(n)) time.
Combining these, the overall time complexity is dominated by the divisor finding part: O(n log n + q * α(n)), which simplifies to O(n log n + q) since α(n) is practically constant.
Space Complexity Analysis:
- The Union-Find data structure requires O(n) space to store the parent and size information for each city.
Therefore, the overall space complexity is O(n).
Code in Different Languages:
The code provided in the problem description already demonstrates the solution in Python, Java, C++, Go and TypeScript. The structure and logic are consistent across all these implementations, reflecting the core Union-Find approach. Each implementation efficiently handles the Union-Find operations and processes the queries.