{x}
blog image

Number of Sets of K Non-Overlapping Line Segments

Given n points on a 1-D plane, where the ith point (from 0 to n-1) is at x = i, find the number of ways we can draw exactly k non-overlapping line segments such that each segment covers two or more points. The endpoints of each segment must have integral coordinates. The k line segments do not have to cover all n points, and they are allowed to share endpoints.

Return the number of ways we can draw k non-overlapping line segments. Since this number can be huge, return it modulo 109 + 7.

 

Example 1:

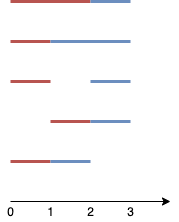
Input: n = 4, k = 2
Output: 5
Explanation: The two line segments are shown in red and blue.
The image above shows the 5 different ways {(0,2),(2,3)}, {(0,1),(1,3)}, {(0,1),(2,3)}, {(1,2),(2,3)}, {(0,1),(1,2)}.

Example 2:

Input: n = 3, k = 1
Output: 3
Explanation: The 3 ways are {(0,1)}, {(0,2)}, {(1,2)}.

Example 3:

Input: n = 30, k = 7
Output: 796297179
Explanation: The total number of possible ways to draw 7 line segments is 3796297200. Taking this number modulo 109 + 7 gives us 796297179.

 

Constraints:

  • 2 <= n <= 1000
  • 1 <= k <= n-1

Solution Explanation

This problem asks to find the number of ways to draw exactly k non-overlapping line segments on n points arranged on a 1D plane. The key to solving this efficiently is using dynamic programming.

Approach:

We define two DP tables:

  • f[i][j]: The number of ways to draw j line segments using the first i points, where the last segment doesn't end at point i.
  • g[i][j]: The number of ways to draw j line segments using the first i points, where the last segment ends at point i.

The recurrence relations are:

  • f[i][j] = f[i-1][j] + g[i-1][j] : We can either extend the current set of segments to i-1 (f[i-1][j]) or add a segment which doesn't end at i (g[i-1][j])

  • g[i][j] = g[i-1][j] + f[i-1][j-1] + g[i-1][j-1] :To end a segment at i, we can extend the segments already ending at i-1 (g[i-1][j]), or add a new segment ending at i with a segment ending at i-1 (f[i-1][j-1] or g[i-1][j-1]).

The base case is f[1][0] = 1 (no segments can be formed with one point). The final answer is (f[n][k] + g[n][k]) % mod, where mod = 10^9 + 7 to handle large numbers.

Time Complexity Analysis:

The DP tables have dimensions (n+1) x (k+1). We iterate through these tables once to fill them. Therefore, the time complexity is O(n*k).

Space Complexity Analysis:

We use two DP tables of size (n+1) x (k+1). Therefore, the space complexity is O(n*k).

Code Explanation (Python):

class Solution:
    def numberOfSets(self, n: int, k: int) -> int:
        mod = 10**9 + 7
        f = [[0] * (k + 1) for _ in range(n + 1)]
        g = [[0] * (k + 1) for _ in range(n + 1)]
        f[1][0] = 1
        for i in range(2, n + 1):
            for j in range(k + 1):
                f[i][j] = (f[i - 1][j] + g[i - 1][j]) % mod
                g[i][j] = g[i - 1][j]
                if j:
                    g[i][j] += f[i - 1][j - 1]
                    g[i][j] %= mod
                    g[i][j] += g[i - 1][j - 1]
                    g[i][j] %= mod
        return (f[-1][-1] + g[-1][-1]) % mod

The code directly implements the recurrence relations described above. The modulo operator (%) is used throughout to prevent integer overflow. The final result is the sum of the last entries in both DP tables, taken modulo 10^9 + 7. The other languages (Java, C++, Go, TypeScript) follow the same logic with only syntax differences.