{x}
blog image

Rank Transform of a Matrix

Given an m x n matrix, return a new matrix answer where answer[row][col] is the rank of matrix[row][col].

The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:

  • The rank is an integer starting from 1.
  • If two elements p and q are in the same row or column, then:
    • If p < q then rank(p) < rank(q)
    • If p == q then rank(p) == rank(q)
    • If p > q then rank(p) > rank(q)
  • The rank should be as small as possible.

The test cases are generated so that answer is unique under the given rules.

 

Example 1:

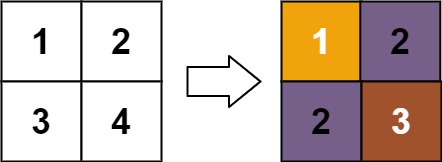
Input: matrix = [[1,2],[3,4]]
Output: [[1,2],[2,3]]
Explanation:
The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column.
The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2.

Example 2:

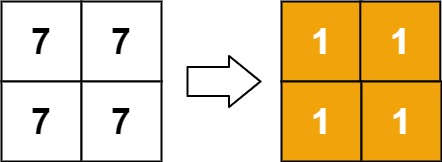
Input: matrix = [[7,7],[7,7]]
Output: [[1,1],[1,1]]

Example 3:

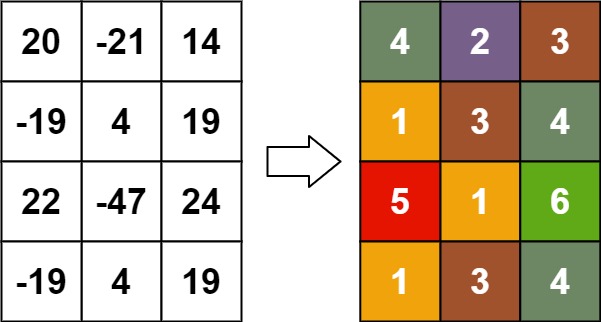
Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

 

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 500
  • -109 <= matrix[row][col] <= 109

Solution Explanation:

This problem requires finding the rank of each element in a matrix based on its relative value within its row and column. The solution uses a Union-Find data structure to efficiently track connected components within the matrix based on element values. Here's a breakdown:

1. Data Structures:

  • Union-Find (Disjoint Set Union): This data structure is crucial for efficiently determining whether elements belong to the same connected component. It uses find() to get the representative element of a set and union() to merge two sets. reset is used to reset the sets after processing elements with the same value.

  • d (Dictionary/Map): Stores the value of each element as a key and a list of its coordinates (row, column) as the value. This allows for efficient iteration through elements of the same value.

  • rowMax and colMax: These arrays track the maximum rank encountered in each row and column respectively.

2. Algorithm:

  1. Initialization:

    • Create a Union-Find data structure with size m + n (rows + columns).
    • Initialize rowMax and colMax arrays with zeros.
    • Create a dictionary/map d to store the value and coordinate of elements in the matrix.

  2. Iteration:

    • Sort the unique element values in ascending order.
    • For each value v:
      • Iterate through the list of coordinates associated with v.
      • Using the Union-Find, unite each cell's row with its column in the union-find data structure. This ensures that cells in the same row or column are in the same set.
      • Find the maximum rank within the connected component of each cell (using rowMax and colMax).
      • Set the rank of the cell to 1 + the maximum rank found in step above.
      • Update rowMax and colMax with the new rank of the cell.
      • Reset the sets in the Union-Find, removing the current value's connections. This prepares the union-find for the next set of values.

  3. Result:

    • The ans matrix stores the calculated ranks, which is then returned.

3. Time Complexity Analysis:

  • Sorting unique values: O(k log k), where k is the number of unique elements in the matrix.
  • Iterating through elements of the same value: O(m*n) in the worst case where all elements have different values.
  • Union-Find operations (find, union, reset): Each operation takes almost constant time on average due to path compression and union by rank optimizations. Thus, these operations contribute O(m*n * α(m+n)) to the complexity, where α(m+n) is the inverse Ackermann function, which is very close to a constant for practical purposes.

Therefore, the overall time complexity is dominated by the sorting and iteration steps, resulting in O(m*n + k log k), where m and n are dimensions of the matrix and k is the number of unique elements in the matrix.

4. Space Complexity Analysis:

  • Union-Find: O(m + n) space.
  • d: O(m*n) in the worst case (all elements are unique).
  • rowMax, colMax, ans: O(m + n) space.
  • Rank array: O(m+n)

Therefore, the overall space complexity is O(m*n).

The provided code in Python, Java, C++, and Go implements this algorithm efficiently. The Union-Find implementation significantly optimizes the connectivity check, making the solution efficient even for large matrices.