- {x}
- Perfect Number
- Most Frequent Subtree Sum
- Fibonacci Number
- Inorder Successor in BST II
- Game Play Analysis I
- Game Play Analysis II
- Find Bottom Left Tree Value
- Freedom Trail
- Find Largest Value in Each Tree Row
- Longest Palindromic Subsequence
- Super Washing Machines
- Coin Change II
- Random Flip Matrix
- Detect Capital
- Longest Uncommon Subsequence I
- Longest Uncommon Subsequence II
- Continuous Subarray Sum
- Read More...

Find Largest Value in Each Tree Row
Given the root of a binary tree, return an array of the largest value in each row of the tree (0-indexed).
Example 1:
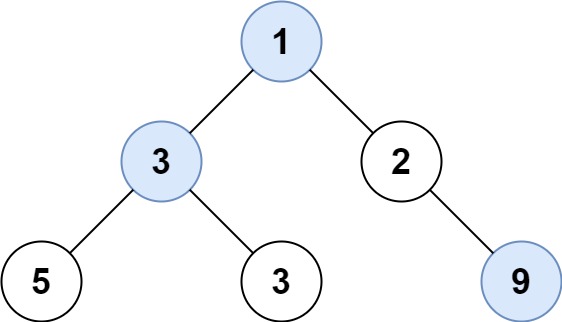
Input: root = [1,3,2,5,3,null,9] Output: [1,3,9]
Example 2:
Input: root = [1,2,3] Output: [1,3]
Constraints:
- The number of nodes in the tree will be in the range
[0, 104]. -231 <= Node.val <= 231 - 1
Solution Explanation for LeetCode 515: Find Largest Value in Each Tree Row
This problem asks to find the largest value in each row of a binary tree. We can solve this using either Breadth-First Search (BFS) or Depth-First Search (DFS).
Approach 1: Breadth-First Search (BFS)
This approach uses a queue to process nodes level by level.
Algorithm:
-
Initialization: Create a queue
qand add the root node to it. Initialize an empty listansto store the largest values of each row. -
Level Processing: While the queue is not empty:
- Get the size
sizeof the queue (number of nodes at the current level). - Initialize a variable
maxValto negative infinity. - Iterate
sizetimes:- Dequeue a node from the queue.
- Update
maxValto the maximum ofmaxValand the node's value. - Enqueue the node's left and right children if they exist.
- Append
maxValtoans.
- Get the size
-
Return: Return
ans.
Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited and processed exactly once.
Space Complexity: O(W), where W is the maximum width of the tree. In the worst case (a complete binary tree), W can be proportional to N. The queue stores nodes from at most one level at a time.
Approach 2: Depth-First Search (DFS)
This approach uses recursion to traverse the tree.
Algorithm:
-
Initialization: Create an empty list
ansto store the largest values of each row. -
Recursive Function
dfs(root, level):- Base Case: If
rootis null, return. - If the current
levelis equal to the size ofans, it means we are encountering a new row, so appendroot.valtoans. - Otherwise, update the value at
ans[level]with the maximum of the current value androot.val. - Recursively call
dfsfor the left and right children withlevel + 1.
- Base Case: If
-
Call dfs: Call
dfs(root, 0)to start the traversal. -
Return: Return
ans.
Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited and processed exactly once.
Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack. In the worst case (a skewed tree), H can be proportional to N.
Code Implementation (Python)
BFS:
from collections import deque
def largestValues(root):
ans = []
if not root:
return ans
q = deque([root])
while q:
size = len(q)
max_val = float('-inf')
for _ in range(size):
node = q.popleft()
max_val = max(max_val, node.val)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
ans.append(max_val)
return ans
DFS:
def largestValues_dfs(root):
ans = []
def dfs(node, level):
if not node:
return
if level == len(ans):
ans.append(node.val)
else:
ans[level] = max(ans[level], node.val)
dfs(node.left, level + 1)
dfs(node.right, level + 1)
dfs(root, 0)
return ans
Both BFS and DFS provide efficient solutions to this problem, with similar time complexities. The choice between them might depend on factors like personal preference, memory constraints (BFS might be slightly better for very wide trees), or whether you need to traverse the tree in a specific order. The provided code snippets show implementations in Python; adapting them to other languages (Java, C++, Go, TypeScript, Rust) is straightforward, using the equivalent data structures (queues, lists, vectors, etc.).