- {x}
- The Maze II
- Relative Ranks
- Perfect Number
- Most Frequent Subtree Sum
- Fibonacci Number
- Inorder Successor in BST II
- Game Play Analysis I
- Game Play Analysis II
- Find Bottom Left Tree Value
- Freedom Trail
- Find Largest Value in Each Tree Row
- Longest Palindromic Subsequence
- Super Washing Machines
- Coin Change II
- Random Flip Matrix
- Detect Capital
- Longest Uncommon Subsequence I
- Read More...

Find Bottom Left Tree Value
Given the root of a binary tree, return the leftmost value in the last row of the tree.
Example 1:
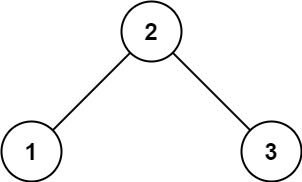
Input: root = [2,1,3] Output: 1
Example 2:
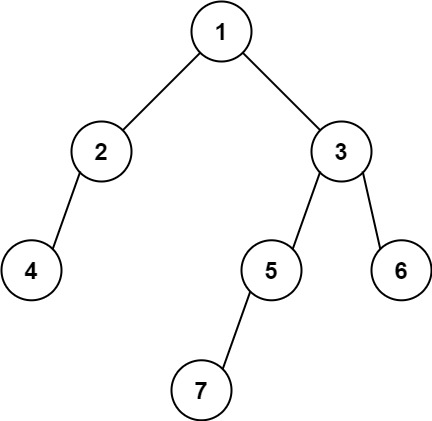
Input: root = [1,2,3,4,null,5,6,null,null,7] Output: 7
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. -231 <= Node.val <= 231 - 1
513. Find Bottom Left Tree Value
This problem asks to find the leftmost value in the last row of a binary tree. We can solve this using either Breadth-First Search (BFS) or Depth-First Search (DFS).
Approach 1: Breadth-First Search (BFS)
This approach is generally more intuitive and efficient for level-order traversal. We use a queue to store nodes level by level. In each level, the first node encountered will be the leftmost node at that level. The last level's leftmost node is our answer.
Algorithm:
-
Initialization: Create a queue
qand add the root node to it. Initialize a variableansto store the leftmost value. -
Level-Order Traversal: While the queue is not empty:
- Update
answith the value of the first node in the queue (this is the leftmost node at the current level). - Process all nodes at the current level: For each node in the queue, remove it from the queue. Add its left child (if it exists) and then its right child (if it exists) to the queue.
- Update
-
Return: After the loop,
ansholds the leftmost value of the last row.
Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited and processed exactly once.
Space Complexity: O(W), where W is the maximum width of the tree. In the worst case (a complete binary tree), W can be equal to N, but in practice it's often much smaller. The space complexity is dominated by the queue used in BFS.
Approach 2: Depth-First Search (DFS)
This approach uses a recursive Depth-First Search. We keep track of the maximum depth encountered so far and the corresponding leftmost value.
Algorithm:
-
Initialization: Initialize
ans(the leftmost value) andmx(the maximum depth) to 0. -
Recursive DFS: Implement a recursive function
dfs(root, curr)that takes the current node and its depthcurras input.- Base Case: If
rootisNone, return. - Recursive Calls: Recursively call
dfsfor the left and right subtrees, incrementing the depth. - Update
ansandmx: If the current depthcurris greater thanmx, it means we've reached a deeper level. Updatemxtocurrandanstoroot.val.
- Base Case: If
-
Return: After the recursive calls finish,
answill contain the leftmost value at the maximum depth.
Time Complexity: O(N), as each node is visited exactly once.
Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack. In the worst case (a skewed tree), H can be equal to N.
Code Examples
The code examples for both approaches are provided in the original response. I'll highlight key aspects:
BFS (Python):
from collections import deque
class Solution:
def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
q = deque([root])
ans = 0
while q:
ans = q[0].val # Leftmost at current level
for _ in range(len(q)):
node = q.popleft()
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
return ansDFS (Python):
class Solution:
def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
ans = mx = 0 # ans: leftmost value, mx: max depth
def dfs(root, curr):
nonlocal ans, mx
if not root: return
dfs(root.left, curr + 1)
dfs(root.right, curr + 1)
if curr > mx: # Found a deeper level
mx = curr
ans = root.val
dfs(root, 1)
return ansThe code in other languages (Java, C++, Go, TypeScript, Rust) follow similar logic and structure to these Python examples. Choose the approach (BFS or DFS) that best suits your understanding and coding style. Generally, BFS is preferred for level-order traversals due to its better space complexity in many practical scenarios.