- {x}
- Least Number of Unique Integers after K Removals
- Minimum Number of Days to Make m Bouquets
- Kth Ancestor of a Tree Node
- Group Sold Products By The Date
- Clone Binary Tree With Random Pointer
- XOR Operation in an Array
- Making File Names Unique
- Avoid Flood in The City
- Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree
- Clone N-ary Tree
- Average Salary Excluding the Minimum and Maximum Salary
- The kth Factor of n
- Longest Subarray of 1's After Deleting One Element
- Parallel Courses II
- Friendly Movies Streamed Last Month
- Path Crossing
- Check If Array Pairs Are Divisible by k
- Read More...

Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree
Given a weighted undirected connected graph with n vertices numbered from 0 to n - 1, and an array edges where edges[i] = [ai, bi, weighti] represents a bidirectional and weighted edge between nodes ai and bi. A minimum spanning tree (MST) is a subset of the graph's edges that connects all vertices without cycles and with the minimum possible total edge weight.
Find all the critical and pseudo-critical edges in the given graph's minimum spanning tree (MST). An MST edge whose deletion from the graph would cause the MST weight to increase is called a critical edge. On the other hand, a pseudo-critical edge is that which can appear in some MSTs but not all.
Note that you can return the indices of the edges in any order.
Example 1:
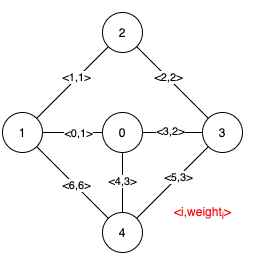
Input: n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]] Output: [[0,1],[2,3,4,5]] Explanation: The figure above describes the graph. The following figure shows all the possible MSTs:Notice that the two edges 0 and 1 appear in all MSTs, therefore they are critical edges, so we return them in the first list of the output. The edges 2, 3, 4, and 5 are only part of some MSTs, therefore they are considered pseudo-critical edges. We add them to the second list of the output.
Example 2:
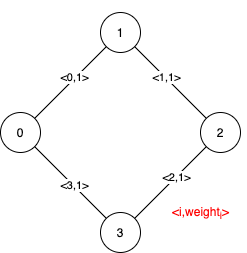
Input: n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]] Output: [[],[0,1,2,3]] Explanation: We can observe that since all 4 edges have equal weight, choosing any 3 edges from the given 4 will yield an MST. Therefore all 4 edges are pseudo-critical.
Constraints:
2 <= n <= 1001 <= edges.length <= min(200, n * (n - 1) / 2)edges[i].length == 30 <= ai < bi < n1 <= weighti <= 1000- All pairs
(ai, bi)are distinct.
Problem Description
The problem asks to find critical and pseudo-critical edges in a Minimum Spanning Tree (MST) of a given graph. A critical edge is an edge in the MST whose removal increases the MST's total weight. A pseudo-critical edge is an edge that can be part of some MSTs but not all.
Solution Explanation
The solution employs a Union-Find data structure to efficiently determine MSTs and their weights. The algorithm iterates through each edge, checking if it's critical or pseudo-critical. The core idea revolves around calculating the MST weight with and without the edge in question.
Steps:
-
Preprocessing: Each edge is augmented with its original index. Edges are then sorted by weight for efficient MST construction.
-
Finding the MST Weight: A Union-Find structure determines the MST weight (
v) by iteratively adding edges (sorted by weight) to the MST, only including those that don't create cycles. -
Critical Edge Check: For each edge, the algorithm creates an MST excluding the edge. If the resulting MST weight is greater than
v(original MST weight), the edge is critical. This means its removal forces a higher-weight edge into the MST. -
Pseudo-Critical Edge Check: For each edge, the algorithm creates an MST including the edge (even if it creates a cycle initially). If the resulting MST weight equals
v(original MST weight), the edge is pseudo-critical. This implies it can be part of an MST, but not necessarily all MSTs.
Data Structures:
- UnionFind: This custom class provides
union(to merge sets) andfind(to check set membership) operations, crucial for efficiently detecting cycles during MST construction.
Time Complexity Analysis:
The algorithm has a time complexity of O(E * (E + α(V))), where:
- E is the number of edges.
- V is the number of vertices.
- α(V) is the inverse Ackermann function (practically a constant for all realistic input sizes).
The O(E) factor comes from iterating through each edge. The O(E + α(V)) factor represents the time complexity of building the MST using Union-Find, which is dominated by the union and find operations. The sort operation takes O(E log E) time. As E < V^2, this is still O(E log E)
Space Complexity Analysis:
The space complexity is O(V + E) due to the Union-Find data structure and the storage of edges and results.
Code Explanation (Python)
class UnionFind:
def __init__(self, n):
self.p = list(range(n))
self.n = n
def union(self, a, b):
if self.find(a) == self.find(b):
return False
self.p[self.find(a)] = self.find(b)
self.n -= 1
return True
def find(self, x):
if self.p[x] != x:
self.p[x] = self.find(self.p[x])
return self.p[x]
class Solution:
def findCriticalAndPseudoCriticalEdges(
self, n: int, edges: List[List[int]]
) -> List[List[int]]:
# Add index to each edge
for i, e in enumerate(edges):
e.append(i)
# Sort edges by weight
edges.sort(key=lambda x: x[2])
# Find MST weight
uf = UnionFind(n)
v = sum(w for f, t, w, _ in edges if uf.union(f, t))
ans = [[], []]
for f, t, w, i in edges:
# Check for critical edges
uf = UnionFind(n)
k = sum(z for x, y, z, j in edges if j != i and uf.union(x, y))
if uf.n > 1 or (uf.n == 1 and k > v):
ans[0].append(i)
continue
#Check for pseudo-critical edges
uf = UnionFind(n)
uf.union(f, t)
k = w + sum(z for x, y, z, j in edges if j != i and uf.union(x, y))
if k == v:
ans[1].append(i)
return ansThe code in other languages (Java, C++, Go) follows the same logic, with minor syntactic differences to accommodate the respective language features. The core algorithm remains consistent across all implementations.