- {x}
- Final Prices With a Special Discount in a Shop
- Subrectangle Queries
- Find Two Non-overlapping Sub-arrays Each With Target Sum
- Allocate Mailboxes
- Sales by Day of the Week
- Running Sum of 1d Array
- Least Number of Unique Integers after K Removals
- Minimum Number of Days to Make m Bouquets
- Kth Ancestor of a Tree Node
- Group Sold Products By The Date
- Clone Binary Tree With Random Pointer
- XOR Operation in an Array
- Making File Names Unique
- Avoid Flood in The City
- Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree
- Clone N-ary Tree
- Average Salary Excluding the Minimum and Maximum Salary
- Read More...

Kth Ancestor of a Tree Node
You are given a tree with n nodes numbered from 0 to n - 1 in the form of a parent array parent where parent[i] is the parent of ith node. The root of the tree is node 0. Find the kth ancestor of a given node.
The kth ancestor of a tree node is the kth node in the path from that node to the root node.
Implement the TreeAncestor class:
TreeAncestor(int n, int[] parent)Initializes the object with the number of nodes in the tree and the parent array.int getKthAncestor(int node, int k)return thekthancestor of the given nodenode. If there is no such ancestor, return-1.
Example 1:
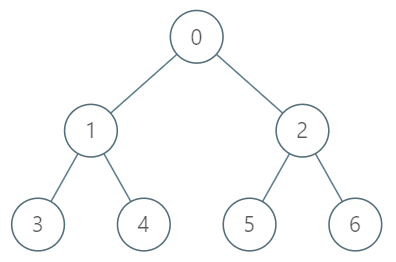
Input ["TreeAncestor", "getKthAncestor", "getKthAncestor", "getKthAncestor"] [[7, [-1, 0, 0, 1, 1, 2, 2]], [3, 1], [5, 2], [6, 3]] Output [null, 1, 0, -1] Explanation TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]); treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3 treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5 treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor
Constraints:
1 <= k <= n <= 5 * 104parent.length == nparent[0] == -10 <= parent[i] < nfor all0 < i < n0 <= node < n- There will be at most
5 * 104queries.
Solution Explanation: 1483. Kth Ancestor of a Tree Node
This problem requires finding the k-th ancestor of a given node in a tree. A brute-force approach of traversing upwards k times is inefficient. The optimal solution uses dynamic programming and binary lifting for efficient ancestor retrieval.
Approach: Dynamic Programming & Binary Lifting
-
Initialization: We create a 2D array
pof sizen x 18, wherenis the number of nodes.p[i][j]stores the 2j-th ancestor of nodei. We initialize the first column (j=0) with the direct parent of each node from the inputparentarray. A value of -1 indicates no parent (for the root or if the kth ancestor doesn't exist). -
Dynamic Programming: We iterate through the remaining columns (
j = 1 to 17). For each nodeiand power of 2j, we compute the 2j-th ancestor by finding the 2j-1-th ancestor of the 2j-1-th ancestor. This is expressed by the recurrence relation:p[i][j] = p[p[i][j-1]][j-1]. This pre-computation allows us to efficiently access higher ancestors later. -
Query (
getKthAncestor): To find the k-th ancestor of a given node, we iterate through the bits of k (from the most significant bit to the least significant bit). If the i-th bit of k is set (meaning k has a 2i component), we jump 2i steps up the tree usingp[node][i]. Ifp[node][i]is -1, it means there is no such ancestor, and we return -1. Otherwise, we update the currentnodeto its 2i-th ancestor and continue to the next bit.
Time Complexity Analysis:
- Initialization: The initialization step iterates through
nnodes and18columns (since 217 >= 50000, which is the maximum number of nodes). Therefore, the time complexity is O(n log n). - Query: The
getKthAncestorfunction iterates through at most log2(k) bits, where k is the desired ancestor level. Since k ≤ n, the time complexity is O(log n).
Space Complexity Analysis:
The space complexity is dominated by the p array, which has dimensions n x 18. Thus, the space complexity is O(n log n).
Code Examples (Python3):
class TreeAncestor:
def __init__(self, n: int, parent: List[int]):
self.p = [[-1] * 18 for _ in range(n)]
for i, fa in enumerate(parent):
self.p[i][0] = fa
for j in range(1, 18):
for i in range(n):
if self.p[i][j - 1] == -1:
continue
self.p[i][j] = self.p[self.p[i][j - 1]][j - 1]
def getKthAncestor(self, node: int, k: int) -> int:
for i in range(17, -1, -1):
if k >> i & 1:
node = self.p[node][i]
if node == -1:
break
return nodeThe code in other languages (Java, C++, Go, TypeScript, C#) follows a very similar structure, reflecting the same algorithm. The only differences are syntax-specific.