{x}
blog image

Path Crossing

Given a string path, where path[i] = 'N', 'S', 'E' or 'W', each representing moving one unit north, south, east, or west, respectively. You start at the origin (0, 0) on a 2D plane and walk on the path specified by path.

Return true if the path crosses itself at any point, that is, if at any time you are on a location you have previously visited. Return false otherwise.

 

Example 1:

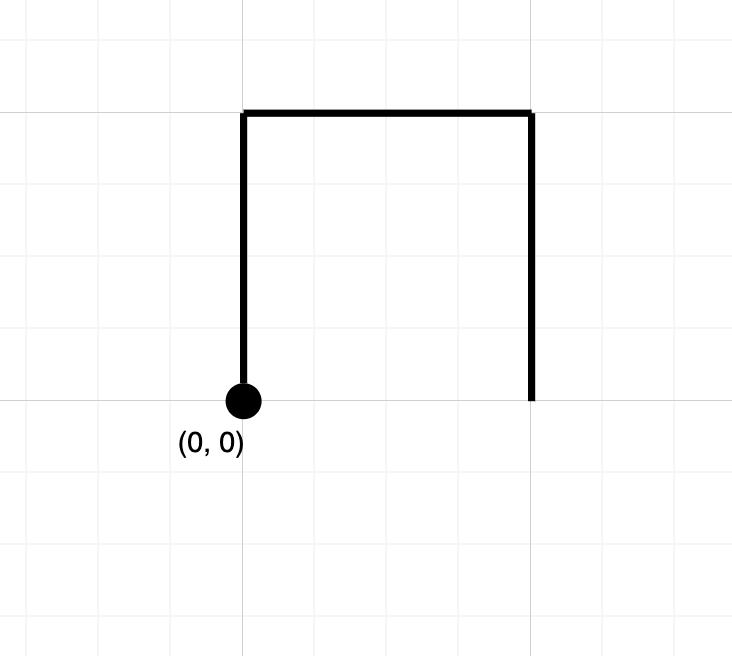
Input: path = "NES"
Output: false 
Explanation: Notice that the path doesn't cross any point more than once.

Example 2:

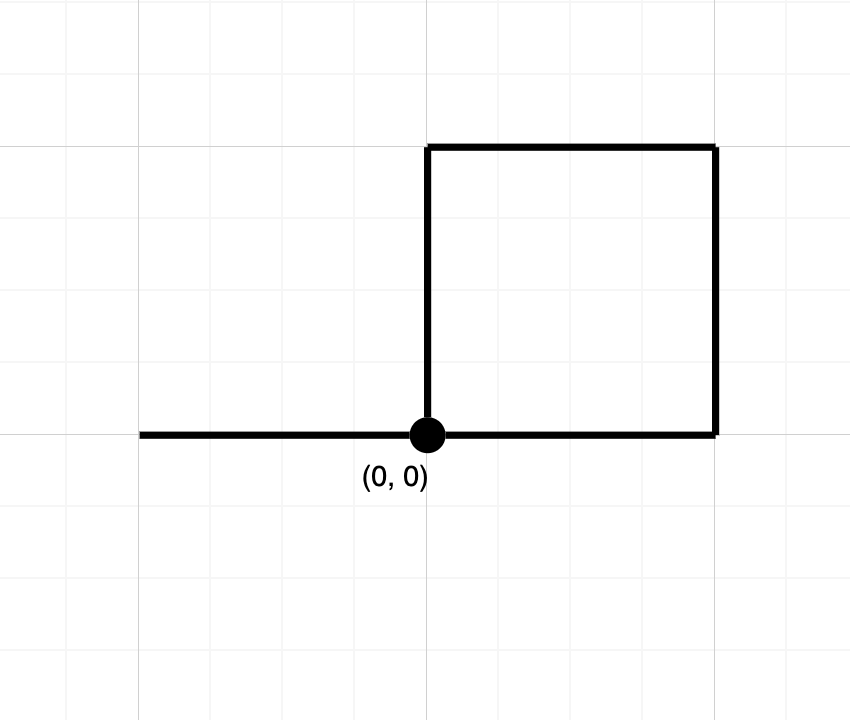
Input: path = "NESWW"
Output: true
Explanation: Notice that the path visits the origin twice.

 

Constraints:

  • 1 <= path.length <= 104
  • path[i] is either 'N', 'S', 'E', or 'W'.

Solution Explanation

This problem asks whether a path, represented by a string of 'N', 'S', 'E', and 'W' characters, crosses itself. The solution involves tracking the current coordinates and checking if they've been visited before.

Approach:

The most efficient approach is to use a hash set (or dictionary in Python) to store the visited coordinates. We start at the origin (0, 0). For each character in the path string:

  1. Update Coordinates: Based on the character ('N', 'S', 'E', 'W'), we update the x and y coordinates accordingly.

  2. Check for Crossing: We check if the current coordinates are already present in the visited set. If they are, it means the path has crossed itself, and we return true.

  3. Add to Visited: If the coordinates are not in the visited set, we add them, and continue to the next character.

  4. Return False: If the loop completes without finding a crossing, we return false.

Time Complexity Analysis:

The time complexity is O(N), where N is the length of the path string. This is because we iterate through the string once. Hash set lookups and insertions are, on average, O(1).

Space Complexity Analysis:

The space complexity is O(N) in the worst case. In the worst case, the path might never cross itself, and we store all the unique coordinates visited in the visited set. The size of the set could be up to N.

Code Explanation (Python):

class Solution:
    def isPathCrossing(self, path: str) -> bool:
        i = j = 0  # Initialize coordinates to (0, 0)
        vis = {(0, 0)}  # Set to store visited coordinates, starting with (0,0)
        for c in path:  # Iterate through each character in the path string
            match c: # python 3.10+ pattern matching
                case 'N':
                    i -= 1
                case 'S':
                    i += 1
                case 'E':
                    j += 1
                case 'W':
                    j -= 1
            if (i, j) in vis:  # Check if current coordinates are already visited
                return True  # If visited, path crosses itself
            vis.add((i, j))  # Add current coordinates to the visited set
        return False  # If loop completes without crossing, return False

The other languages (Java, C++, Go, TypeScript) follow a similar approach, using the appropriate data structures for sets in each language. The core logic remains the same. The Java, C++, and Go examples use a more compact representation of the coordinates within the hash set to improve efficiency. They use a single integer to represent the coordinate pair (e.g., i * 20000 + j). This is a common optimization when dealing with coordinate pairs and hash sets. The constant 20000 ensures a unique integer representation for reasonable coordinate values. Choosing an appropriate constant depends on the constraints of the problem (in this case, the constraint on path length helps determine this).