- {x}
- XOR Operation in an Array
- Making File Names Unique
- Avoid Flood in The City
- Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree
- Clone N-ary Tree
- Average Salary Excluding the Minimum and Maximum Salary
- The kth Factor of n
- Longest Subarray of 1's After Deleting One Element
- Parallel Courses II
- Friendly Movies Streamed Last Month
- Path Crossing
- Check If Array Pairs Are Divisible by k
- Number of Subsequences That Satisfy the Given Sum Condition
- Max Value of Equation
- Design a File Sharing System
- Countries You Can Safely Invest In
- Can Make Arithmetic Progression From Sequence
- Read More...

Parallel Courses II
You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCoursei, nextCoursei], representing a prerequisite relationship between course prevCoursei and course nextCoursei: course prevCoursei has to be taken before course nextCoursei. Also, you are given the integer k.
In one semester, you can take at most k courses as long as you have taken all the prerequisites in the previous semesters for the courses you are taking.
Return the minimum number of semesters needed to take all courses. The testcases will be generated such that it is possible to take every course.
Example 1:
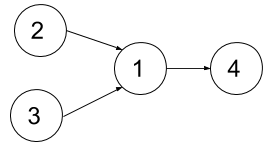
Input: n = 4, relations = [[2,1],[3,1],[1,4]], k = 2 Output: 3 Explanation: The figure above represents the given graph. In the first semester, you can take courses 2 and 3. In the second semester, you can take course 1. In the third semester, you can take course 4.
Example 2:
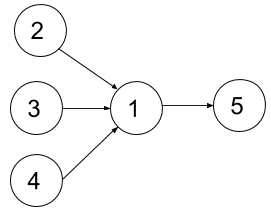
Input: n = 5, relations = [[2,1],[3,1],[4,1],[1,5]], k = 2 Output: 4 Explanation: The figure above represents the given graph. In the first semester, you can only take courses 2 and 3 since you cannot take more than two per semester. In the second semester, you can take course 4. In the third semester, you can take course 1. In the fourth semester, you can take course 5.
Constraints:
1 <= n <= 151 <= k <= n0 <= relations.length <= n * (n-1) / 2relations[i].length == 21 <= prevCoursei, nextCoursei <= nprevCoursei != nextCoursei- All the pairs
[prevCoursei, nextCoursei]are unique. - The given graph is a directed acyclic graph.
Solution Explanation:
This problem can be solved using bit manipulation and breadth-first search (BFS). The core idea is to represent the courses taken in each semester using a bitmask. Each bit in the bitmask corresponds to a course; if the bit is set, the course has been taken.
1. Preprocessing:
- We create a
darray (or equivalent data structure in other languages) to store the prerequisites for each course.d[i]represents a bitmask where each set bit indicates a prerequisite course for coursei. This is done by iterating through therelationsarray.
2. BFS:
- We start with an initial state where no courses have been taken (bitmask 0).
- The BFS queue
qstores pairs(current_state, semesters_taken). - In each iteration, we:
- Check if all courses have been taken (
current_state == (1 << (n + 1)) - 2). If so, we have found the solution. - Calculate
nxt, a bitmask representing the courses that can be taken in the current semester. A course can be taken if all its prerequisites are already satisfied (checked using bitwise AND withd[i]).nxtis then XORed withcurto get only the courses that haven't been taken. - Course Selection: If the number of courses in
nxtis less than or equal tok, we can take all of them in this semester. Otherwise, we need to choose a subset ofkcourses fromnxt. This is where the bit manipulation gets slightly more complex. We iterate through all possible subsets ofnxtusing bit manipulation (subtracting 1 and bitwise ANDing). For each subset, we check if its size iskand if it hasn't been visited before. - Add the new state (updated bitmask) and increased semester count to the queue if it hasn't been visited before.
- Check if all courses have been taken (
3. Bit Manipulation Subset Generation:
The key part of the code is the generation of subsets of size k when nxt has more courses than k. It's done using a clever bit manipulation technique:
x = nxt
while nxt:
if nxt.bit_count() == k and (nxt | cur) not in vis:
q.append((nxt | cur, t + 1))
nxt = (nxt - 1) & x
This loop iterates through all possible subsets of x. nxt = (nxt - 1) & x is the crucial part. Let's break down how it works:
nxt - 1: Decrements the bitmask. This flips the least significant set bit to 0 and sets all bits to the right to 1.& x: The bitwise AND with the originalxkeeps only the bits that were originally set inx. Effectively, this systematically removes one bit at a time from the originalxand generates all possible subsets.
Time Complexity Analysis:
The time complexity is dominated by the BFS. In the worst case, we could explore all possible states, which is O(2n). The subset generation loop within each BFS step can also add to the complexity but remains within the same order because the number of subsets is also bounded by O(2n).
Space Complexity Analysis:
The space complexity is dominated by the vis set which stores visited states and the queue q. In the worst case, both can store up to O(2n) states.
Therefore, the overall time and space complexity are both O(2n) in the worst case. However, because n is limited to 15 in the problem constraints, this algorithm remains efficient enough to solve the problem.