- {x}
- Count Unguarded Cells in the Grid
- Escape the Spreading Fire
- Remove Digit From Number to Maximize Result
- Minimum Consecutive Cards to Pick Up
- K Divisible Elements Subarrays
- Total Appeal of A String
- Make Array Non-decreasing or Non-increasing
- Largest 3-Same-Digit Number in String
- Count Nodes Equal to Average of Subtree
- Count Number of Texts
- Check if There Is a Valid Parentheses String Path
- Minimum Number of Keypresses
- Find the K-Beauty of a Number
- Number of Ways to Split Array
- Maximum White Tiles Covered by a Carpet
- Substring With Largest Variance
- Find Resultant Array After Removing Anagrams
- Read More...

Count Nodes Equal to Average of Subtree
Given the root of a binary tree, return the number of nodes where the value of the node is equal to the average of the values in its subtree.
Note:
- The average of
nelements is the sum of thenelements divided bynand rounded down to the nearest integer. - A subtree of
rootis a tree consisting ofrootand all of its descendants.
Example 1:
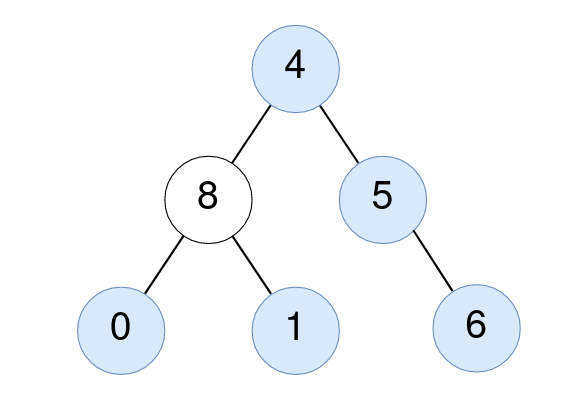
Input: root = [4,8,5,0,1,null,6] Output: 5 Explanation: For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4. For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5. For the node with value 0: The average of its subtree is 0 / 1 = 0. For the node with value 1: The average of its subtree is 1 / 1 = 1. For the node with value 6: The average of its subtree is 6 / 1 = 6.
Example 2:

Input: root = [1] Output: 1 Explanation: For the node with value 1: The average of its subtree is 1 / 1 = 1.
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. 0 <= Node.val <= 1000
Solution: Count Nodes Equal to Average of Subtree
This problem involves traversing a binary tree and determining the number of nodes where the node's value is equal to the average of its subtree's values. The average is rounded down to the nearest integer.
Approach:
The most efficient way to solve this is using Depth-First Search (DFS). We'll perform a post-order traversal of the tree. For each node, we'll recursively calculate the sum and count of nodes in its subtree. Then, we check if the node's value is equal to the average of its subtree.
Algorithm:
-
dfs(node)function: This recursive function takes a node as input and returns a pair:(subtree_sum, subtree_node_count). -
Base Case: If
nodeisnull, return(0, 0). -
Recursive Step:
- Recursively call
dfs()on the left and right children to get their subtree sums and counts (left_sum,left_count,right_sum,right_count). - Calculate the total sum of the current node's subtree:
subtree_sum = left_sum + right_sum + node.val. - Calculate the total count of nodes in the current node's subtree:
subtree_count = left_count + right_count + 1. - Check if
node.valis equal tosubtree_sum // subtree_count(integer division). If they are equal, increment a global counterans. - Return
(subtree_sum, subtree_count).
- Recursively call
-
Main Function:
- Initialize a global counter
ansto 0. - Call
dfs(root). - Return
ans.
- Initialize a global counter
Time Complexity: O(N), where N is the number of nodes in the tree. We visit each node exactly once.
Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack. In the worst case (a skewed tree), H can be N, but in a balanced tree, H is log₂N.
Code Implementation (Python):
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def averageOfSubtree(self, root: TreeNode) -> int:
self.ans = 0 # Global counter
def dfs(node):
if not node:
return 0, 0 # Sum, Count
left_sum, left_count = dfs(node.left)
right_sum, right_count = dfs(node.right)
subtree_sum = left_sum + right_sum + node.val
subtree_count = left_count + right_count + 1
if node.val == subtree_sum // subtree_count:
self.ans += 1
return subtree_sum, subtree_count
dfs(root)
return self.ansCode Implementation (Java):
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
int ans = 0;
public int averageOfSubtree(TreeNode root) {
dfs(root);
return ans;
}
private int[] dfs(TreeNode node) {
if (node == null) return new int[]{0, 0}; // Sum, Count
int[] left = dfs(node.left);
int[] right = dfs(node.right);
int subtreeSum = left[0] + right[0] + node.val;
int subtreeCount = left[1] + right[1] + 1;
if (node.val == subtreeSum / subtreeCount) ans++;
return new int[]{subtreeSum, subtreeCount};
}
}Similar implementations can be done in other languages like C++, JavaScript, etc., following the same algorithmic structure. The key is the post-order traversal and efficient calculation of subtree sums and counts.