{x}
blog image

Maximum White Tiles Covered by a Carpet

You are given a 2D integer array tiles where tiles[i] = [li, ri] represents that every tile j in the range li <= j <= ri is colored white.

You are also given an integer carpetLen, the length of a single carpet that can be placed anywhere.

Return the maximum number of white tiles that can be covered by the carpet.

 

Example 1:

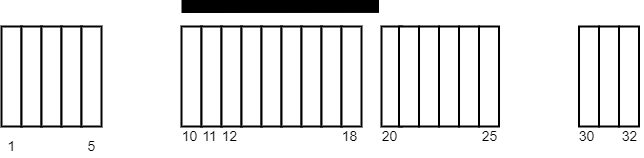
Input: tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10
Output: 9
Explanation: Place the carpet starting on tile 10. 
It covers 9 white tiles, so we return 9.
Note that there may be other places where the carpet covers 9 white tiles.
It can be shown that the carpet cannot cover more than 9 white tiles.

Example 2:

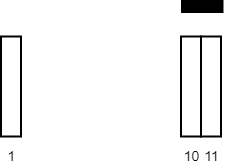
Input: tiles = [[10,11],[1,1]], carpetLen = 2
Output: 2
Explanation: Place the carpet starting on tile 10. 
It covers 2 white tiles, so we return 2.

 

Constraints:

  • 1 <= tiles.length <= 5 * 104
  • tiles[i].length == 2
  • 1 <= li <= ri <= 109
  • 1 <= carpetLen <= 109
  • The tiles are non-overlapping.

Solution Explanation:

This problem asks to find the maximum number of white tiles that can be covered by a carpet of a given length. The solution uses a two-pointer approach combined with sorting and prefix sums implicitly.

Algorithm:

  1. Sort: The tiles array is sorted based on the starting position (l<sub>i</sub>) of each tile. This allows for efficient processing as we traverse the tiles in ascending order of their starting positions.

  2. Two Pointers: Two pointers, i and j, are used to maintain a sliding window. i represents the starting position of the carpet, and j iterates through tiles that are potentially covered by the carpet.

  3. Window Maintenance:

    • The inner while loop expands the window (j increments) as long as the entire length of the tiles from tiles[i][0] to tiles[j][1] is less than or equal to carpetLen. During this expansion, the total number of white tiles (s) covered by the current carpet position is updated.
    • The if condition checks if extending the carpet beyond tiles[j] would cover more white tiles. If it does, the ans is updated.

  4. Sliding Window: After processing tiles covered by the carpet starting at tiles[i], the outer loop increments i, effectively shifting the carpet to the right. The number of tiles covered by the tile at i is subtracted from the running total s before moving to the next tile.

  5. Return: The maximum number of covered white tiles (ans) is returned.

Time Complexity: O(N log N), where N is the number of tiles. The dominant factor is the sorting step. The two-pointer approach itself has a linear time complexity.

Space Complexity: O(1). The algorithm uses a constant amount of extra space, regardless of the input size. It modifies the input array in-place.

Example Walkthrough (Python):

Let's trace the Python code with the example: tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10

  1. tiles is sorted: [[1, 5], [10, 11], [12, 18], [20, 25], [30, 32]]

  2. The loop starts:

    • i = 0, j = 0, s = 0, ans = 0. The inner loop adds [1, 5] (s = 5). j becomes 1.
    • The condition tiles[j][1] - tiles[i][0] + 1 <= carpetLen (11 - 1 + 1 <= 10) is false, so the inner loop stops. ans becomes max(0, 5) = 5. s is reset to 0.
    • i = 1. The inner loop adds [10,11] (s=2), [12,18] (s = 2 + 7 = 9), j becomes 3.
    • tiles[j][1] - tiles[i][0] + 1 (25 - 10 + 1 = 16 > 10). The inner loop stops. ans becomes max(5, 9) = 9. s is updated.
    • This process continues until all tiles are checked, and ans holds the maximum number of covered tiles.

The code in other languages (Java, C++, Go) follows the same algorithm with minor syntactic differences. The key idea is the efficient use of two pointers and sorting to find the optimal carpet placement.