- {x}
- Stone Game IV
- Customer Order Frequency
- Number of Good Pairs
- Number of Substrings With Only 1s
- Path with Maximum Probability
- Best Position for a Service Centre
- Move Sub-Tree of N-Ary Tree
- Find Users With Valid E-Mails
- Water Bottles
- Number of Nodes in the Sub-Tree With the Same Label
- Maximum Number of Non-Overlapping Substrings
- Find a Value of a Mysterious Function Closest to Target
- Diameter of N-Ary Tree
- Count Odd Numbers in an Interval Range
- Number of Sub-arrays With Odd Sum
- Number of Good Ways to Split a String
- Minimum Number of Increments on Subarrays to Form a Target Array
- Read More...

Water Bottles
There are numBottles water bottles that are initially full of water. You can exchange numExchange empty water bottles from the market with one full water bottle.
The operation of drinking a full water bottle turns it into an empty bottle.
Given the two integers numBottles and numExchange, return the maximum number of water bottles you can drink.
Example 1:
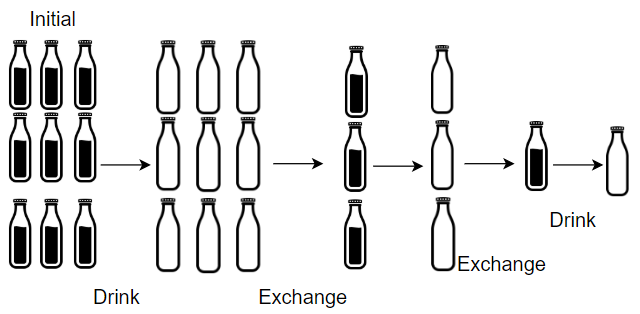
Input: numBottles = 9, numExchange = 3 Output: 13 Explanation: You can exchange 3 empty bottles to get 1 full water bottle. Number of water bottles you can drink: 9 + 3 + 1 = 13.
Example 2:
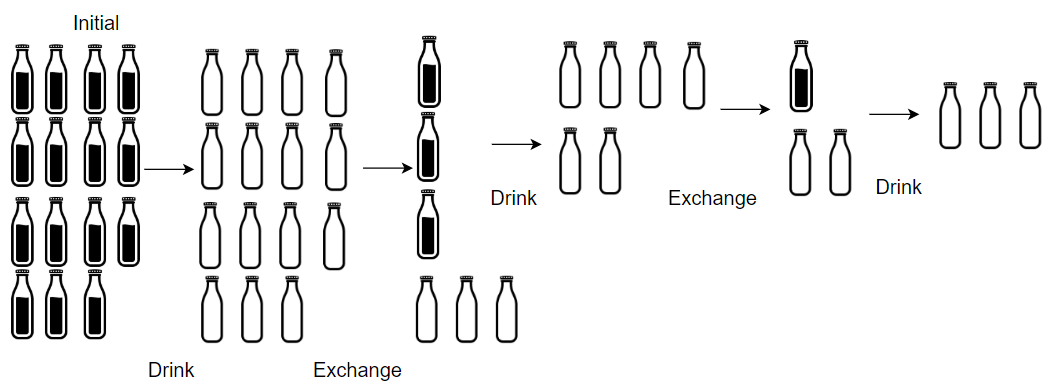
Input: numBottles = 15, numExchange = 4 Output: 19 Explanation: You can exchange 4 empty bottles to get 1 full water bottle. Number of water bottles you can drink: 15 + 3 + 1 = 19.
Constraints:
1 <= numBottles <= 1002 <= numExchange <= 100
Solution Explanation
The problem involves calculating the maximum number of water bottles you can drink given an initial number of bottles and the exchange rate for empty bottles. The solution utilizes a simple iterative approach.
Approach:
-
Initialization: The total number of bottles drunk (
ans) is initialized to the initial number of full bottles (numBottles). -
Iteration: The loop continues as long as the number of empty bottles is greater than or equal to the exchange rate (
numExchange). In each iteration:- We calculate the number of additional bottles obtained from exchanging empty bottles:
numBottles / numExchange. - The total number of drunk bottles (
ans) is increased by this number. - The number of full bottles is updated by subtracting the exchanged bottles and adding the newly obtained bottles.
- We calculate the number of additional bottles obtained from exchanging empty bottles:
-
Return Value: The function returns
ans, representing the total number of water bottles drunk.
Code Explanation (Python Example):
class Solution:
def numWaterBottles(self, numBottles: int, numExchange: int) -> int:
ans = numBottles
while numBottles >= numExchange:
empty_bottles = numBottles // numExchange # Integer division to find the number of new bottles
ans += empty_bottles # Add the number of new bottles to the total
numBottles = numBottles % numExchange + empty_bottles # Update the number of bottles.
return ans
Time and Space Complexity Analysis:
-
Time Complexity: O(log n), where n is
numBottles. The loop iterates untilnumBottlesbecomes less thannumExchange. In each iteration,numBottlesis reduced significantly, resulting in a logarithmic time complexity. In the worst case, it will be O(n) if numExchange is 2. -
Space Complexity: O(1). The algorithm uses only a constant amount of extra space to store variables, regardless of the input size.
Example Walkthrough (Python):
Let's say numBottles = 9 and numExchange = 3.
ansis initialized to 9.- The loop starts:
- Iteration 1:
numBottles(9) >=numExchange(3).empty_bottles= 9 // 3 = 3.ansbecomes 9 + 3 = 12.numBottlesbecomes 9 % 3 + 3 = 3. - Iteration 2:
numBottles(3) >=numExchange(3).empty_bottles= 3 // 3 = 1.ansbecomes 12 + 1 = 13.numBottlesbecomes 3 % 3 + 1 = 1. - The loop terminates because
numBottles(1) <numExchange(3).
- Iteration 1:
- The function returns
ans, which is 13.
The provided code in other languages follows the same logic and complexity. The only differences are syntactic variations specific to each programming language.