{x}
blog image

Tree of Coprimes

There is a tree (i.e., a connected, undirected graph that has no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges. Each node has a value associated with it, and the root of the tree is node 0.

To represent this tree, you are given an integer array nums and a 2D array edges. Each nums[i] represents the ith node's value, and each edges[j] = [uj, vj] represents an edge between nodes uj and vj in the tree.

Two values x and y are coprime if gcd(x, y) == 1 where gcd(x, y) is the greatest common divisor of x and y.

An ancestor of a node i is any other node on the shortest path from node i to the root. A node is not considered an ancestor of itself.

Return an array ans of size n, where ans[i] is the closest ancestor to node i such that nums[i] and nums[ans[i]] are coprime, or -1 if there is no such ancestor.

 

Example 1:

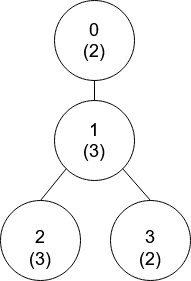
Input: nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
Output: [-1,0,0,1]
Explanation: In the above figure, each node's value is in parentheses.
- Node 0 has no coprime ancestors.
- Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1).
- Node 2 has two ancestors, nodes 1 and 0. Node 1's value is not coprime (gcd(3,3) == 3), but node 0's
  value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor.
- Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its
  closest valid ancestor.

Example 2:

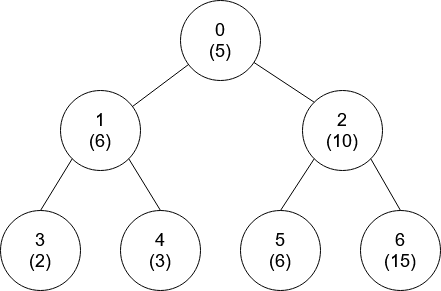
Input: nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
Output: [-1,0,-1,0,0,0,-1]

 

Constraints:

  • nums.length == n
  • 1 <= nums[i] <= 50
  • 1 <= n <= 105
  • edges.length == n - 1
  • edges[j].length == 2
  • 0 <= uj, vj < n
  • uj != vj

Solution Explanation: Tree of Coprimes

This problem involves finding the closest ancestor of each node in a tree whose value is coprime with the node's value. The solution leverages Depth-First Search (DFS) and pre-processing to optimize the search.

1. Preprocessing:

  • Coprime Pairs: We precompute all pairs of numbers (from 1 to 50) that are coprime. This is done using the greatest common divisor (GCD) function. The result is stored in a data structure (e.g., a list of lists, a map) for quick lookup during the DFS traversal. This avoids redundant GCD calculations during the main algorithm.

2. Depth-First Search (DFS):

The core of the solution is a DFS traversal of the tree. For each node, we perform the following:

  • Find Closest Coprime Ancestor: During DFS, we keep track of the visited ancestors and their depths. We use a stack (or similar data structure) for each possible coprime number. When visiting a node i, we check if any of its ancestors (stored in the stacks corresponding to coprime numbers of nums[i]) are coprime with nums[i]. The ancestor with the greatest depth (i.e., closest to node i) is selected as the closest coprime ancestor.
  • Update Stacks: As we move down the tree in the DFS, we push the current node and its depth onto relevant stacks (stacks representing coprime numbers of the current node). When we backtrack (return from a recursive call), we pop the node from the stacks to maintain only the ancestors currently on the path.

3. Time and Space Complexity:

  • Time Complexity: The preprocessing step takes O(M^2) time, where M is the maximum value in nums (50 in this case). The DFS traversal takes O(N) time, where N is the number of nodes in the tree. The search for the closest coprime ancestor within the stacks for each node has a time complexity of O(M), in the worst case. Therefore, the overall time complexity is approximately O(M^2 + N * M).

  • Space Complexity: The preprocessing step requires O(M^2) space to store the coprime pairs. The DFS uses a stack whose maximum size is proportional to the tree's height (which is at most N). Each node in the tree stores at most M stacks of depth proportional to the height, leading to O(N * M) space complexity for the stacks. The overall space complexity is O(M^2 + N * M).

Code Example (Python):

import math
 
def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a % b)
 
def getCoprimes(nums, edges):
    n = len(nums)
    graph = [[] for _ in range(n)]
    for u, v in edges:
        graph[u].append(v)
        graph[v].append(u)
 
    coprimes = [[False] * 51 for _ in range(51)]  # Precompute coprime pairs
    for i in range(1, 51):
        for j in range(1, 51):
            if gcd(i, j) == 1:
                coprimes[i][j] = True
 
    ans = [-1] * n
    ancestor_stacks = [[] for _ in range(51)] #Stack for each possible coprime number
 
    def dfs(node, parent, depth):
        closest_ancestor = -1
        max_depth = -1
        for i in range(1, 51):
            if coprimes[nums[node]][i]: #Check coprimes of current node value
                for anc, d in ancestor_stacks[i]:
                    if d > max_depth:
                        max_depth = d
                        closest_ancestor = anc
        ans[node] = closest_ancestor
 
        for child in graph[node]:
            if child != parent:
                for i in range(1, 51):
                    if coprimes[nums[node]][i]:
                        ancestor_stacks[i].append((node,depth))
                dfs(child, node, depth + 1)
                for i in range(1, 51):
                    if coprimes[nums[node]][i]:
                        ancestor_stacks[i].pop()
 
    dfs(0, -1, 0)
    return ans

The code in other languages (Java, C++, Go) follows a similar structure, employing DFS and pre-computation of coprime pairs for efficiency. The key difference lies in the implementation details related to data structures (e.g., stacks, adjacency lists).