{x}
blog image

Minimum Degree of a Connected Trio in a Graph

You are given an undirected graph. You are given an integer n which is the number of nodes in the graph and an array edges, where each edges[i] = [ui, vi] indicates that there is an undirected edge between ui and vi.

A connected trio is a set of three nodes where there is an edge between every pair of them.

The degree of a connected trio is the number of edges where one endpoint is in the trio, and the other is not.

Return the minimum degree of a connected trio in the graph, or -1 if the graph has no connected trios.

 

Example 1:

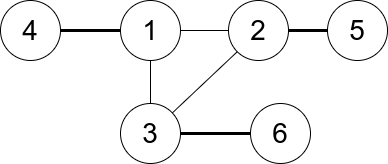
Input: n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
Output: 3
Explanation: There is exactly one trio, which is [1,2,3]. The edges that form its degree are bolded in the figure above.

Example 2:

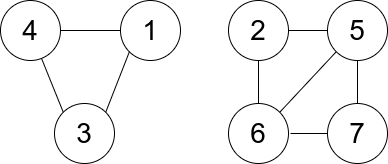
Input: n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
Output: 0
Explanation: There are exactly three trios:
1) [1,4,3] with degree 0.
2) [2,5,6] with degree 2.
3) [5,6,7] with degree 2.

 

Constraints:

  • 2 <= n <= 400
  • edges[i].length == 2
  • 1 <= edges.length <= n * (n-1) / 2
  • 1 <= ui, vi <= n
  • ui != vi
  • There are no repeated edges.

Minimum Degree of a Connected Trio in a Graph

This problem asks to find the minimum degree of a connected trio in an undirected graph. A connected trio is a set of three nodes where there's an edge between every pair. The degree of a connected trio is the number of edges connecting one node in the trio to a node outside the trio.

Approach

The most straightforward approach is brute force enumeration. We iterate through all possible triplets of nodes and check if they form a connected trio. If they do, we calculate the degree of the trio and update the minimum degree found so far.

  1. Adjacency Matrix: We represent the graph using an adjacency matrix g. g[i][j] = true if there's an edge between nodes i and j, otherwise false.

  2. Degree Calculation: We also calculate the degree of each node (deg[i]) – the number of edges connected to node i.

  3. Trio Enumeration: We iterate through all possible combinations of three nodes (i, j, k) where i < j < k.

  4. Trio Check: For each triplet, we verify if it's a connected trio by checking if g[i][j], g[i][k], and g[j][k] are all true.

  5. Degree Calculation for Trio: If it's a trio, we calculate its degree as deg[i] + deg[j] + deg[k] - 6. We subtract 6 because the three edges within the trio are counted three times each in the sum of individual node degrees.

  6. Minimum Degree Update: We update the minimum degree (ans) found so far.

  7. Return Value: If no connected trio is found (ans remains unchanged), we return -1; otherwise, we return ans.

Time and Space Complexity

  • Time Complexity: O(n³), where n is the number of nodes. This is due to the three nested loops iterating through all possible triplets of nodes.

  • Space Complexity: O(n²), dominated by the adjacency matrix g.

Code Implementation (Python)

def minTrioDegree(n: int, edges: List[List[int]]) -> int:
    g = [[False] * n for _ in range(n)]
    deg = [0] * n
    for u, v in edges:
        u -= 1  # Adjust to 0-based indexing
        v -= 1
        g[u][v] = g[v][u] = True
        deg[u] += 1
        deg[v] += 1
 
    ans = float('inf')  # Initialize with positive infinity
    for i in range(n):
        for j in range(i + 1, n):
            if g[i][j]:
                for k in range(j + 1, n):
                    if g[i][k] and g[j][k]:
                        ans = min(ans, deg[i] + deg[j] + deg[k] - 6)
 
    return -1 if ans == float('inf') else ans

The code in other languages (Java, C++, Go, TypeScript) follows the same logic with minor syntax variations. The core algorithm remains the brute-force approach described above. For significantly larger graphs, more optimized algorithms might be necessary, but for the given constraints (n ≤ 400), this brute-force solution is efficient enough.