{x}
blog image

Map of Highest Peak

You are given an integer matrix isWater of size m x n that represents a map of land and water cells.

  • If isWater[i][j] == 0, cell (i, j) is a land cell.
  • If isWater[i][j] == 1, cell (i, j) is a water cell.

You must assign each cell a height in a way that follows these rules:

  • The height of each cell must be non-negative.
  • If the cell is a water cell, its height must be 0.
  • Any two adjacent cells must have an absolute height difference of at most 1. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).

Find an assignment of heights such that the maximum height in the matrix is maximized.

Return an integer matrix height of size m x n where height[i][j] is cell (i, j)'s height. If there are multiple solutions, return any of them.

 

Example 1:

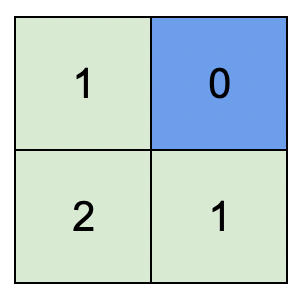
Input: isWater = [[0,1],[0,0]]
Output: [[1,0],[2,1]]
Explanation: The image shows the assigned heights of each cell.
The blue cell is the water cell, and the green cells are the land cells.

Example 2:

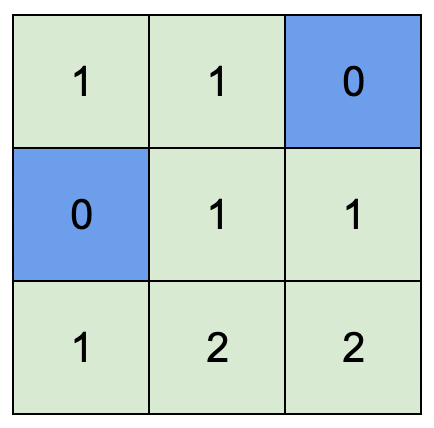
Input: isWater = [[0,0,1],[1,0,0],[0,0,0]]
Output: [[1,1,0],[0,1,1],[1,2,2]]
Explanation: A height of 2 is the maximum possible height of any assignment.
Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.

 

Constraints:

  • m == isWater.length
  • n == isWater[i].length
  • 1 <= m, n <= 1000
  • isWater[i][j] is 0 or 1.
  • There is at least one water cell.

 

Note: This question is the same as 542: https://leetcode.com/problems/01-matrix/

Solution Explanation:

The problem asks to assign heights to cells in a matrix representing land and water, such that:

  1. Water cells have height 0.
  2. Land cells have non-negative heights.
  3. Adjacent cells have a height difference of at most 1.
  4. The maximum height in the matrix is maximized.

The optimal solution involves a Breadth-First Search (BFS) algorithm. The idea is to start from all water cells (height 0) and expand outwards, incrementing the height by 1 for each adjacent land cell. This guarantees that the height difference between adjacent cells is at most 1, and the maximum height is maximized because we explore all possible heights in a level-order manner.

Algorithm:

  1. Initialization: Create a result matrix ans initialized with -1 for land cells and 0 for water cells. Use a queue q to store the coordinates of water cells.

  2. BFS: While the queue is not empty:

    • Dequeue a cell (i, j).
    • For each of its four neighbors:
      • If the neighbor is a land cell (value -1 in ans) and within the matrix bounds:
        • Assign the neighbor a height of ans[i][j] + 1.
        • Enqueue the neighbor.

  3. Return: Return the ans matrix.

Time and Space Complexity Analysis:

  • Time Complexity: O(M*N), where M and N are the dimensions of the matrix. Each cell is visited and processed at most once during the BFS.
  • Space Complexity: O(M*N) in the worst case, to store the result matrix ans and the queue q which could hold all the cells if the entire map is land. In the best case (only water cells), space complexity is O(W), where W is the number of water cells.

Code Implementation:

The code implementations provided use slightly different approaches to handle the queue and neighbor traversal, but all follow the core BFS algorithm. The main difference between Solution 1 and Solution 2 lies in how the queue is processed in each iteration. Solution 1 processes one cell at a time, while Solution 2 processes all cells added in the previous level before moving to the next level. Both solutions achieve the same result, but Solution 2 might be slightly more efficient in practice as it avoids unnecessary queue operations. The choice between these two solutions is often a matter of personal preference or specific optimization needs. The key is that the BFS structure remains consistent in both.

Each code snippet provided shows the implementation in Python, Java, C++, Go, TypeScript, and Rust, all showcasing the BFS approach effectively. The comments within the code enhance readability and understanding. The pairwise function in the Python solution (used for efficient neighbor traversal) can be easily implemented or replaced with explicit neighbor checks in other languages.