- {x}
- Best Sightseeing Pair
- Smallest Integer Divisible by K
- Binary String With Substrings Representing 1 To N
- Convert to Base -2
- Binary Prefix Divisible By 5
- Next Greater Node In Linked List
- Number of Enclaves
- Remove Outermost Parentheses
- Sum of Root To Leaf Binary Numbers
- Camelcase Matching
- Video Stitching
- Divisor Game
- Maximum Difference Between Node and Ancestor
- Longest Arithmetic Subsequence
- Recover a Tree From Preorder Traversal
- Two City Scheduling
- Matrix Cells in Distance Order
- Read More...

Sum of Root To Leaf Binary Numbers
You are given the root of a binary tree where each node has a value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit.
- For example, if the path is
0 -> 1 -> 1 -> 0 -> 1, then this could represent01101in binary, which is13.
For all leaves in the tree, consider the numbers represented by the path from the root to that leaf. Return the sum of these numbers.
The test cases are generated so that the answer fits in a 32-bits integer.
Example 1:
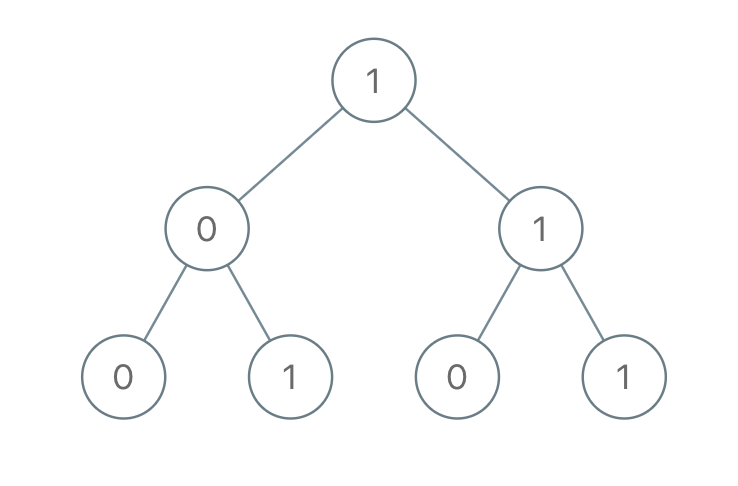
Input: root = [1,0,1,0,1,0,1] Output: 22 Explanation: (100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22
Example 2:
Input: root = [0] Output: 0
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. Node.valis0or1.
1022. Sum of Root To Leaf Binary Numbers
Problem Description
Given the root of a binary tree where each node has a value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit. The task is to find the sum of all numbers represented by these root-to-leaf paths.
Solution: Depth-First Search (DFS)
The most efficient approach to solve this problem is using Depth-First Search (DFS). We recursively traverse the tree, building the binary number as we go down each path.
Algorithm
- Base Case: If the current node is
null, return 0 (no contribution to the sum). - Update Current Number: Shift the current binary number (
current_num) to the left by 1 bit (current_num << 1) and add the current node's value (current_num | node.val). - Leaf Node Check: If the current node is a leaf node (no left or right children), return the
current_num. This is a complete binary number from root to leaf. - Recursive Calls: Recursively call the function for the left and right children, adding their results to get the total sum for the current subtree.
Time and Space Complexity Analysis
- Time Complexity: O(N), where N is the number of nodes in the tree. We visit each node exactly once.
- Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack. In the worst case (a skewed tree), H can be equal to N. In a balanced tree, H is log(N).
Code Implementation (Python)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumRootToLeaf(self, root: TreeNode) -> int:
def dfs(node, current_num):
if not node:
return 0
current_num = (current_num << 1) | node.val
if not node.left and not node.right: # Leaf node
return current_num
return dfs(node.left, current_num) + dfs(node.right, current_num)
return dfs(root, 0)Code Implementation (Java)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int sumRootToLeaf(TreeNode root) {
return dfs(root, 0);
}
private int dfs(TreeNode node, int current_num) {
if (node == null) return 0;
current_num = (current_num << 1) | node.val;
if (node.left == null && node.right == null) return current_num;
return dfs(node.left, current_num) + dfs(node.right, current_num);
}
}Code Implementation (C++)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int sumRootToLeaf(TreeNode* root) {
return dfs(root, 0);
}
int dfs(TreeNode* node, int current_num) {
if (!node) return 0;
current_num = (current_num << 1) | node->val;
if (!node->left && !node->right) return current_num;
return dfs(node->left, current_num) + dfs(node->right, current_num);
}
};The implementations in other languages (Go, TypeScript, Rust) would follow a similar structure, adapting the syntax to the specific language. The core algorithm remains the same efficient DFS approach.