- {x}
- Binary Prefix Divisible By 5
- Next Greater Node In Linked List
- Number of Enclaves
- Remove Outermost Parentheses
- Sum of Root To Leaf Binary Numbers
- Camelcase Matching
- Video Stitching
- Divisor Game
- Maximum Difference Between Node and Ancestor
- Longest Arithmetic Subsequence
- Recover a Tree From Preorder Traversal
- Two City Scheduling
- Matrix Cells in Distance Order
- Maximum Sum of Two Non-Overlapping Subarrays
- Stream of Characters
- Moving Stones Until Consecutive
- Coloring A Border
- Read More...

Maximum Difference Between Node and Ancestor
Given the root of a binary tree, find the maximum value v for which there exist different nodes a and b where v = |a.val - b.val| and a is an ancestor of b.
A node a is an ancestor of b if either: any child of a is equal to b or any child of a is an ancestor of b.
Example 1:
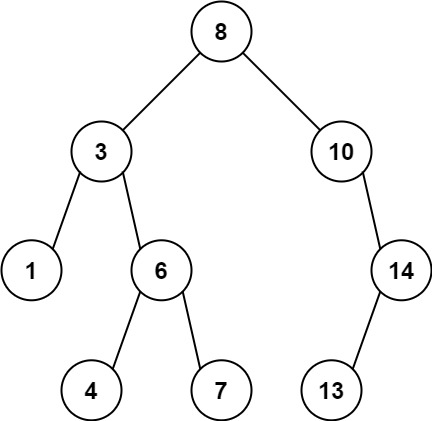
Input: root = [8,3,10,1,6,null,14,null,null,4,7,13] Output: 7 Explanation: We have various ancestor-node differences, some of which are given below : |8 - 3| = 5 |3 - 7| = 4 |8 - 1| = 7 |10 - 13| = 3 Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
Example 2:
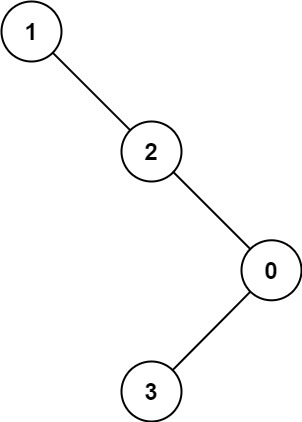
Input: root = [1,null,2,null,0,3] Output: 3
Constraints:
- The number of nodes in the tree is in the range
[2, 5000]. 0 <= Node.val <= 105
Solution Explanation: Maximum Difference Between Node and Ancestor
This problem asks to find the maximum absolute difference between the value of a node and the value of one of its ancestors in a binary tree.
Approach: Depth-First Search (DFS)
The most efficient way to solve this is using a Depth-First Search (DFS) approach. We traverse the tree recursively, keeping track of the minimum and maximum values encountered so far along each path from the root. For each node, we calculate the difference between its value and the current minimum and maximum values. The largest such difference becomes our answer.
Algorithm
-
DFS Function: Create a recursive function
dfs(node, min_val, max_val)that takes the current node, the minimum value encountered so far (min_val), and the maximum value encountered so far (max_val) as input. -
Base Case: If the current
nodeis null (we've reached the end of a branch), return. -
Update Maximum Difference: Calculate the absolute differences between the current node's value (
node.val) andmin_val, andnode.valandmax_val. Update the global maximum difference (max_diff) if a larger difference is found. -
Update Min and Max: Update
min_valandmax_valto include the current node's value:min_val = min(min_val, node.val)andmax_val = max(max_val, node.val). -
Recursive Calls: Recursively call
dfsfor the left and right children of the current node, passing the updatedmin_valandmax_val. -
Initial Call: Start the DFS by calling
dfs(root, root.val, root.val). The initialmin_valandmax_valare both the root's value because the root has no ancestors. -
Return: After the DFS completes, the
max_diffvariable will hold the maximum difference.
Time and Space Complexity Analysis
- Time Complexity: O(N), where N is the number of nodes in the tree. We visit each node exactly once.
- Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack. In the worst case (a skewed tree), H can be equal to N. In a balanced tree, H is log₂(N).
Code Examples (Python, Java, C++, Go, TypeScript, JavaScript, C#)
The code examples in multiple languages provided earlier demonstrate this algorithm effectively. Each version follows the same fundamental steps outlined above. The differences are mainly syntactical. Note that helper functions like min, max, and abs are used as appropriate for each language. The use of a global or class variable (ans or max_diff) to track the maximum difference is crucial for storing the result across recursive calls.