- {x}
- Capacity To Ship Packages Within D Days
- Numbers With Repeated Digits
- Partition Array Into Three Parts With Equal Sum
- Best Sightseeing Pair
- Smallest Integer Divisible by K
- Binary String With Substrings Representing 1 To N
- Convert to Base -2
- Binary Prefix Divisible By 5
- Next Greater Node In Linked List
- Number of Enclaves
- Remove Outermost Parentheses
- Sum of Root To Leaf Binary Numbers
- Camelcase Matching
- Video Stitching
- Divisor Game
- Maximum Difference Between Node and Ancestor
- Longest Arithmetic Subsequence
- Read More...

Next Greater Node In Linked List
You are given the head of a linked list with n nodes.
For each node in the list, find the value of the next greater node. That is, for each node, find the value of the first node that is next to it and has a strictly larger value than it.
Return an integer array answer where answer[i] is the value of the next greater node of the ith node (1-indexed). If the ith node does not have a next greater node, set answer[i] = 0.
Example 1:
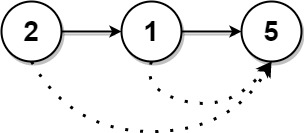
Input: head = [2,1,5] Output: [5,5,0]
Example 2:
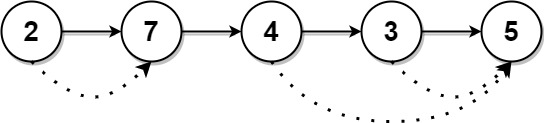
Input: head = [2,7,4,3,5] Output: [7,0,5,5,0]
Constraints:
- The number of nodes in the list is
n. 1 <= n <= 1041 <= Node.val <= 109
1019. Next Greater Node In Linked List
Problem Description
Given the head of a linked list, find the value of the next greater node for each node. The next greater node for a given node is the first node to its right with a strictly larger value. If no such node exists, the next greater node is 0. Return an array where the i-th element is the value of the next greater node of the i-th node (1-indexed).
Solution: Monotonic Stack
This problem can be efficiently solved using a monotonic stack. A monotonic stack is a stack where the elements are always in increasing or decreasing order. In this case, we'll use a decreasing monotonic stack.
Algorithm:
- Convert Linked List to Array: First, traverse the linked list and store the node values in an array
nums. - Initialize Stack and Result Array: Create an empty stack
stkand an arrayansof the same size asnums, initialized with zeros.answill store the result. - Iterate Backwards: Iterate through
numsfrom right to left (indexifromn-1to 0, wherenis the length ofnums). - Monotonic Stack Processing: For each element
nums[i]:- While the stack is not empty and the top element of the stack (
stk[-1]) is less than or equal tonums[i], pop elements from the stack. This ensures that the stack maintains a decreasing order. - If the stack is not empty after popping, the top element of the stack is the next greater node for
nums[i]. Assign this value toans[i]. - Push
nums[i]onto the stack.
- While the stack is not empty and the top element of the stack (
- Return Result: After iterating through all elements,
anscontains the next greater node values for each node. Returnans.
Time and Space Complexity
- Time Complexity: O(n), where n is the number of nodes in the linked list. We iterate through the array once. The stack operations (push and pop) take constant time on average.
- Space Complexity: O(n) in the worst case, to store the
numsarray and the stack. In the best-case scenario where the linked list is already in decreasing order, the stack space would be minimal.
Code Implementation (Python)
class Solution:
def nextLargerNodes(self, head: ListNode) -> List[int]:
nums = []
while head:
nums.append(head.val)
head = head.next
stk = []
n = len(nums)
ans = [0] * n
for i in range(n - 1, -1, -1):
while stk and stk[-1] <= nums[i]:
stk.pop()
if stk:
ans[i] = stk[-1]
stk.append(nums[i])
return ans
The code in other languages (Java, C++, Go, TypeScript, Rust, Javascript) follows a very similar structure, adapting the syntax and data structures to each language's specifics, but maintaining the same core algorithm. The fundamental idea of using a decreasing monotonic stack to efficiently find the next greater element remains consistent across all implementations.