- {x}
- Similar String Groups
- Magic Squares In Grid
- Keys and Rooms
- Split Array into Fibonacci Sequence
- Guess the Word
- Backspace String Compare
- Longest Mountain in Array
- Hand of Straights
- Shortest Path Visiting All Nodes
- Shifting Letters
- Maximize Distance to Closest Person
- Rectangle Area II
- Loud and Rich
- Peak Index in a Mountain Array
- Car Fleet
- K-Similar Strings
- Exam Room
- Read More...

Shortest Path Visiting All Nodes
You have an undirected, connected graph of n nodes labeled from 0 to n - 1. You are given an array graph where graph[i] is a list of all the nodes connected with node i by an edge.
Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
Example 1:
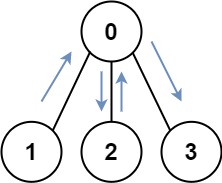
Input: graph = [[1,2,3],[0],[0],[0]] Output: 4 Explanation: One possible path is [1,0,2,0,3]
Example 2:
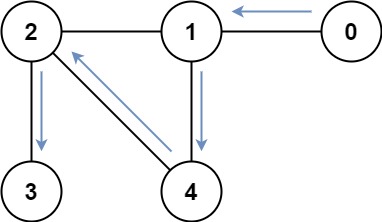
Input: graph = [[1],[0,2,4],[1,3,4],[2],[1,2]] Output: 4 Explanation: One possible path is [0,1,4,2,3]
Constraints:
n == graph.length1 <= n <= 120 <= graph[i].length < ngraph[i]does not containi.- If
graph[a]containsb, thengraph[b]containsa. - The input graph is always connected.
Solution Explanation for Shortest Path Visiting All Nodes
This problem asks for the length of the shortest path that visits every node in an undirected, connected graph. We can solve this using Breadth-First Search (BFS) and bit manipulation.
Approach:
The key idea is to represent the state of our traversal using a bitmask. Each bit in the bitmask corresponds to a node in the graph. If the i-th bit is set, it means we've visited node i. Our BFS will explore states, moving from one node to another until we reach a state where all bits are set (meaning all nodes have been visited).
-
Initialization:
- We start the BFS from every node.
- The initial state for each node is a bitmask with only the corresponding bit set (representing that only that node has been visited initially).
- We use a
visitedset to track visited states to avoid cycles.
-
BFS Traversal:
- In each iteration of the BFS, we process all states in the current level of the queue.
- For each state
(currentNode, currentStateBitmask), we explore all neighbors ofcurrentNode. - For each neighbor
neighborNode, we create a new state(neighborNode, newStateBitmask), wherenewStateBitmaskis the result of setting the bit corresponding toneighborNodeincurrentStateBitmask. - If this new state hasn't been visited, we add it to the queue and mark it as visited.
-
Termination:
- The BFS terminates when we find a state whose bitmask has all bits set. This represents a path that has visited all nodes.
- The distance (number of edges) at that point is the length of the shortest path.
Time Complexity Analysis:
- The number of possible states is
O(n * 2^n), wherenis the number of nodes. Each node can be the starting point, and there are2^npossible subsets of nodes visited. - In the worst case, the BFS might visit all possible states.
- Therefore, the time complexity is O(n * 2^n).
Space Complexity Analysis:
- The space complexity is dominated by the queue and the
visitedset, which in the worst case can store all possible states. - Therefore, the space complexity is O(n * 2^n).
Code Explanation (Python):
from collections import deque
class Solution:
def shortestPathLength(self, graph: List[List[int]]) -> int:
n = len(graph)
q = deque()
visited = set()
# Initialize the queue with all nodes as starting points
for i in range(n):
q.append((i, 1 << i)) # (node, bitmask)
visited.add((i, 1 << i))
ans = 0
while q:
level_size = len(q)
for _ in range(level_size):
curr_node, curr_state = q.popleft()
if curr_state == (1 << n) - 1: # All nodes visited
return ans
# Explore neighbors
for neighbor in graph[curr_node]:
next_state = curr_state | (1 << neighbor)
if (neighbor, next_state) not in visited:
visited.add((neighbor, next_state))
q.append((neighbor, next_state))
ans += 1 # Increment distance for each level
return -1 #Should not reach here if graph is connected.
The code in other languages (Java, C++, Go, TypeScript, Rust) follows a very similar structure, using the same core algorithm of BFS and bit manipulation. They differ slightly in syntax and data structures used (e.g., Deque vs. queue, Set vs. HashSet, etc.). The time and space complexity remain the same.