{x}
blog image

Maximize Distance to Closest Person

You are given an array representing a row of seats where seats[i] = 1 represents a person sitting in the ith seat, and seats[i] = 0 represents that the ith seat is empty (0-indexed).

There is at least one empty seat, and at least one person sitting.

Alex wants to sit in the seat such that the distance between him and the closest person to him is maximized. 

Return that maximum distance to the closest person.

 

Example 1:

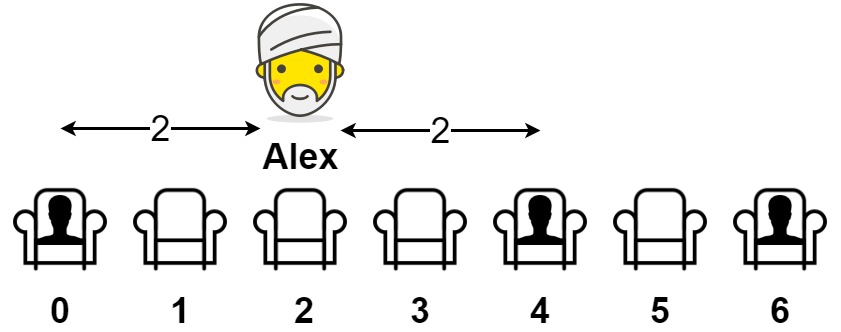
Input: seats = [1,0,0,0,1,0,1]
Output: 2
Explanation: 
If Alex sits in the second open seat (i.e. seats[2]), then the closest person has distance 2.
If Alex sits in any other open seat, the closest person has distance 1.
Thus, the maximum distance to the closest person is 2.

Example 2:

Input: seats = [1,0,0,0]
Output: 3
Explanation: 
If Alex sits in the last seat (i.e. seats[3]), the closest person is 3 seats away.
This is the maximum distance possible, so the answer is 3.

Example 3:

Input: seats = [0,1]
Output: 1

 

Constraints:

  • 2 <= seats.length <= 2 * 104
  • seats[i] is 0 or 1.
  • At least one seat is empty.
  • At least one seat is occupied.

Solution Explanation for Maximize Distance to Closest Person

This problem asks to find the maximum distance to the closest person if you were to sit in an empty seat. The solution involves a single pass through the seats array.

Approach:

The core idea is to track the distances between occupied seats. The maximum distance to the closest person will either be:

  1. The largest gap between two occupied seats (divided by 2): This accounts for the scenario where an empty seat is surrounded by people.
  2. The distance from the first empty seat to the nearest person on the left: This handles the edge case where the beginning of the array has empty seats.
  3. The distance from the last empty seat to the nearest person on the right: Similar to point 2, but handling the end of the array.

Algorithm:

  1. Initialization:

    • first: Stores the index of the first occupied seat (-1 initially).
    • last: Stores the index of the last occupied seat seen (-1 initially).
    • max_dist: Stores the maximum distance between two occupied seats (0 initially).

  2. Iteration:

    • Iterate through the seats array.
    • If seats[i] == 1 (occupied seat):
      • If last is not -1 (meaning this is not the first occupied seat), calculate the distance to the previously seen occupied seat (i - last) and update max_dist if necessary.
      • If first is -1 (meaning this is the first occupied seat), update first.
      • Update last to the current index i.

  3. Result:

    • The maximum distance is the largest of:
      • max_dist // 2 (integer division): The largest gap divided by 2.
      • first: Distance from the beginning to the first person.
      • len(seats) - last - 1: Distance from the end to the last person.

Time Complexity: O(n), where n is the length of the seats array. We iterate through the array once.

Space Complexity: O(1). We use only a constant number of extra variables.

Code Examples:

The code provided in the original response demonstrates this algorithm efficiently in Python, Java, C++, Go, and TypeScript. The logic in each is consistent with the algorithm described above. The key differences are primarily in syntax and handling of variables (e.g., null vs -1, use of max function).

Example Walkthrough (Python):

Let's consider seats = [1,0,0,0,1,0,1].

  1. The loop starts.
  2. seats[0] == 1, first becomes 0, last becomes 0.
  3. seats[4] == 1, i - last = 4 - 0 = 4, max_dist becomes 4. last becomes 4.
  4. seats[6] == 1, i - last = 6 - 4 = 2, max_dist remains 4, last becomes 6.
  5. The loop ends.
  6. max(4 // 2, 0, 7 - 6 - 1) = max(2, 0, 0) = 2. The function returns 2.

The other languages follow the same core logic, adapting to their specific syntax and data type handling.