{x}
blog image

Rectangle Area II

You are given a 2D array of axis-aligned rectangles. Each rectangle[i] = [xi1, yi1, xi2, yi2] denotes the ith rectangle where (xi1, yi1) are the coordinates of the bottom-left corner, and (xi2, yi2) are the coordinates of the top-right corner.

Calculate the total area covered by all rectangles in the plane. Any area covered by two or more rectangles should only be counted once.

Return the total area. Since the answer may be too large, return it modulo 109 + 7.

 

Example 1:

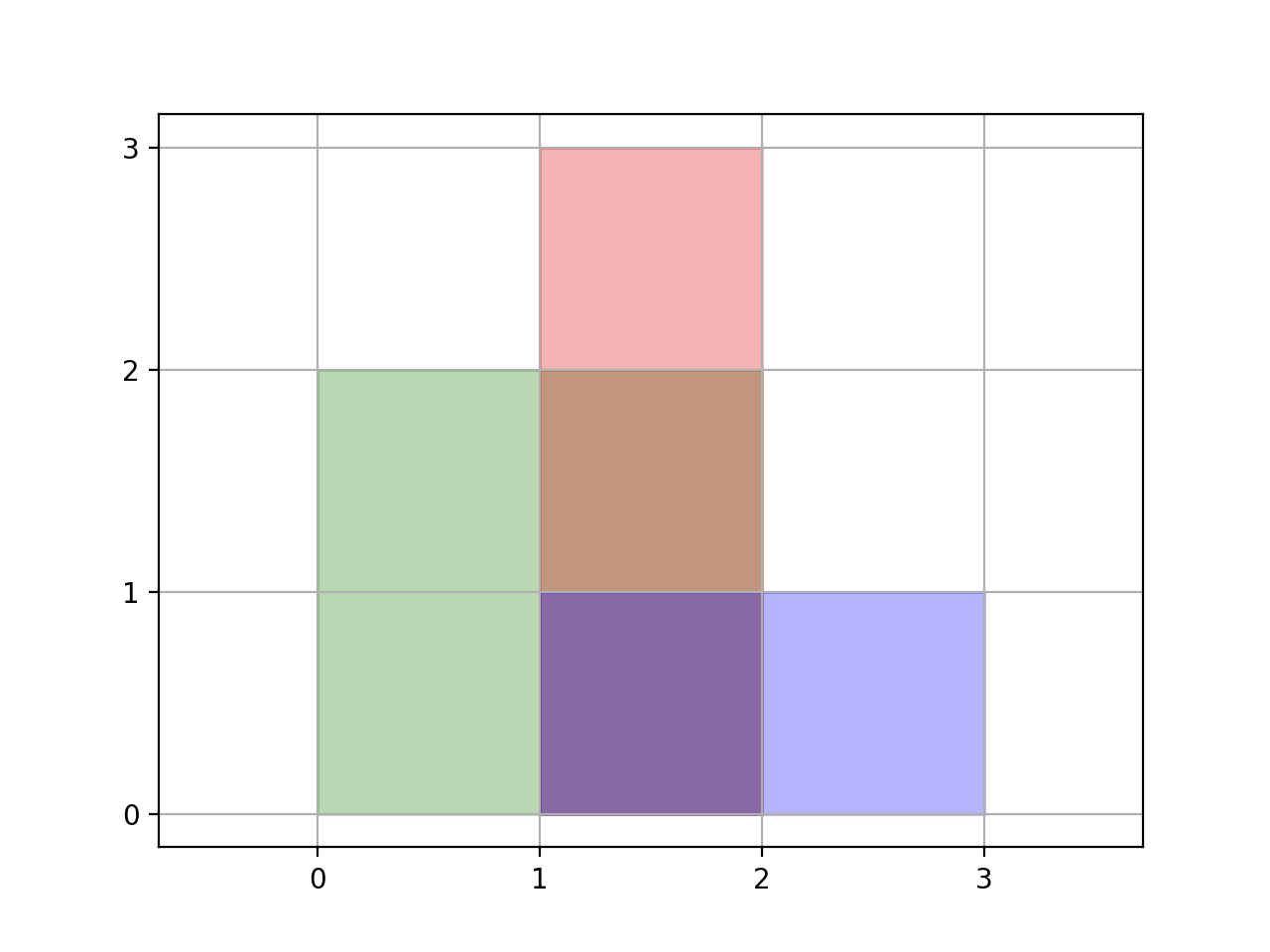
Input: rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
Output: 6
Explanation: A total area of 6 is covered by all three rectangles, as illustrated in the picture.
From (1,1) to (2,2), the green and red rectangles overlap.
From (1,0) to (2,3), all three rectangles overlap.

Example 2:

Input: rectangles = [[0,0,1000000000,1000000000]]
Output: 49
Explanation: The answer is 1018 modulo (109 + 7), which is 49.

 

Constraints:

  • 1 <= rectangles.length <= 200
  • rectanges[i].length == 4
  • 0 <= xi1, yi1, xi2, yi2 <= 109
  • xi1 <= xi2
  • yi1 <= yi2
  • All rectangles have non zero area.

Solution Explanation for Rectangle Area II

This problem asks to calculate the total area covered by a set of overlapping rectangles. A naive approach of calculating the area of each rectangle and summing them would be incorrect because it double-counts overlapping areas. The optimal solution uses a line sweep algorithm combined with a segment tree.

Algorithm:

  1. Event Points: We first identify all unique x-coordinates from the given rectangles. These will be our "event points" in the line sweep.

  2. Line Sweep: We iterate through the sorted event points. For each x-coordinate:

    • We process all rectangles that either start or end at that x-coordinate.
    • We update a segment tree that tracks the intervals along the y-axis that are covered by rectangles.

  3. Segment Tree: The segment tree efficiently maintains the total length of the y-intervals covered by rectangles at each x-coordinate. Each node in the segment tree represents a range of y-values. The cnt field of a node indicates how many rectangles cover that range. The length field indicates the total length of the y-intervals covered within that node.

  4. Area Calculation: The area between consecutive x-coordinates is simply the length of the y-intervals covered (obtained from the segment tree) multiplied by the difference between the x-coordinates. We sum these areas to get the final total area.

Time Complexity:

  • Sorting: Sorting the event points takes O(N log N) time, where N is the number of rectangles.
  • Line Sweep: Iterating through the event points takes O(N) time.
  • Segment Tree Operations: Each segment tree operation (modify and query) takes O(log M) time, where M is the number of unique y-coordinates. In the worst case, M can be O(N).
  • Overall: The overall time complexity is dominated by the sorting step, resulting in O(N log N).

Space Complexity:

  • Segment Tree: The segment tree requires O(M) space, where M is the number of unique y-coordinates. In the worst case, M can be O(N).
  • Other Data Structures: The space used for storing event points and other data structures is also O(N).
  • Overall: The overall space complexity is O(N).

Code Explanation (Python):

The Python code implements the algorithm as follows:

  1. Node class: Represents a node in the segment tree. It tracks the start and end y-coordinates (l, r), the count of overlapping rectangles (cnt), and the covered length (length).

  2. SegmentTree class: Implements the segment tree data structure with build, modify, and pushup methods for building, updating, and propagating changes through the tree, respectively. The length property returns the total covered length.

  3. Solution.rectangleArea: This function orchestrates the line sweep algorithm. It:

    • Extracts unique x and y coordinates.
    • Sorts events (x-coordinates with rectangle start/end indicators).
    • Builds the segment tree.
    • Iterates through sorted events, updating the segment tree and accumulating areas.
    • Returns the total area modulo 109 + 7.

The Java, C++, and Go codes follow a very similar structure and logic, implementing the same algorithm with language-specific syntax and data structures. The core concepts of the line sweep algorithm and the segment tree remain consistent across all languages.