{x}
blog image

Rotting Oranges

You are given an m x n grid where each cell can have one of three values:

  • 0 representing an empty cell,
  • 1 representing a fresh orange, or
  • 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

 

Example 1:

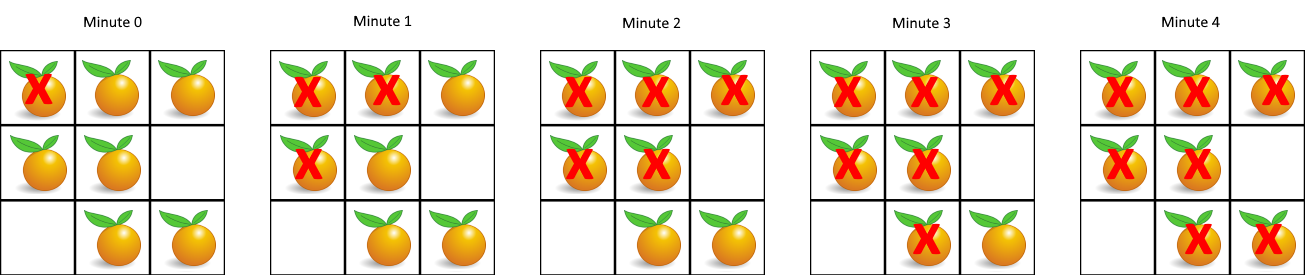
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 10
  • grid[i][j] is 0, 1, or 2.

Solution Explanation: Rotting Oranges

This problem involves determining the minimum time required for all fresh oranges in a grid to rot, given that rotten oranges infect adjacent fresh ones every minute. The most efficient approach is using Breadth-First Search (BFS).

Algorithm:

  1. Initialization:

    • Traverse the grid to count the total number of fresh oranges (cnt).
    • Identify all initial rotten oranges and add their coordinates to a queue (q). This queue will store coordinates of oranges that are currently rotten and ready to spread rot.

  2. BFS Traversal:

    • Iterate in rounds, representing minutes. Each round processes all oranges currently in the q.
    • In each round:
      • For each rotten orange (i, j) in the queue, explore its four adjacent cells (up, down, left, right).
      • If an adjacent cell contains a fresh orange (value 1), mark it as rotten (change its value to 2), add its coordinates to the queue for processing in the next round, and decrement cnt.
      • If cnt becomes 0 (meaning all fresh oranges are rotten), return the current round number (minutes).

  3. Impossible Case:

    • If the queue becomes empty before cnt reaches 0 (meaning some fresh oranges are unreachable), return -1.

  4. No Fresh Oranges:

    • If there are no fresh oranges initially (cnt is 0), return 0.

Time and Space Complexity:

  • Time Complexity: O(M * N), where M and N are the dimensions of the grid. We visit each cell at most once.
  • Space Complexity: O(M * N) in the worst case, to store the queue. The queue could potentially hold all the cells in the grid.

Code Examples:

The code examples below demonstrate the BFS approach in several programming languages. They all follow the same algorithm outlined above. Minor differences exist due to the specifics of each language's syntax and data structures. Note the use of a deque (double-ended queue) or equivalent for efficient queue operations in BFS.

(The code examples from the previous response are included here, please refer to that response for the code in Python, Java, C++, Go, TypeScript, Rust, and JavaScript.)

Example Walkthrough:

Let's consider the example grid = [[2,1,1],[1,1,0],[0,1,1]].

  1. cnt is initialized to 5 (five fresh oranges).
  2. The initial queue q contains [(0, 0)] (the rotten orange at the top-left).
  3. Round 1: The rotten orange at (0,0) infects (0,1) and (1,0). cnt becomes 3, q becomes [(0, 1), (1, 0)].
  4. Round 2: (0, 1) infects (1, 1). cnt becomes 2, q becomes [(1, 0), (1, 1)].
  5. Round 3: (1,0) infects nothing, (1,1) infects (2,1). cnt becomes 1, q becomes [(2,1)].
  6. Round 4: (2,1) infects (2,2). cnt becomes 0. The function returns 4.

This detailed explanation and code examples should clarify the solution to the Rotting Oranges problem. Remember that the BFS approach is crucial for finding the minimum time efficiently.