{x}
blog image

Grid Illumination

There is a 2D grid of size n x n where each cell of this grid has a lamp that is initially turned off.

You are given a 2D array of lamp positions lamps, where lamps[i] = [rowi, coli] indicates that the lamp at grid[rowi][coli] is turned on. Even if the same lamp is listed more than once, it is turned on.

When a lamp is turned on, it illuminates its cell and all other cells in the same row, column, or diagonal.

You are also given another 2D array queries, where queries[j] = [rowj, colj]. For the jth query, determine whether grid[rowj][colj] is illuminated or not. After answering the jth query, turn off the lamp at grid[rowj][colj] and its 8 adjacent lamps if they exist. A lamp is adjacent if its cell shares either a side or corner with grid[rowj][colj].

Return an array of integers ans, where ans[j] should be 1 if the cell in the jth query was illuminated, or 0 if the lamp was not.

 

Example 1:

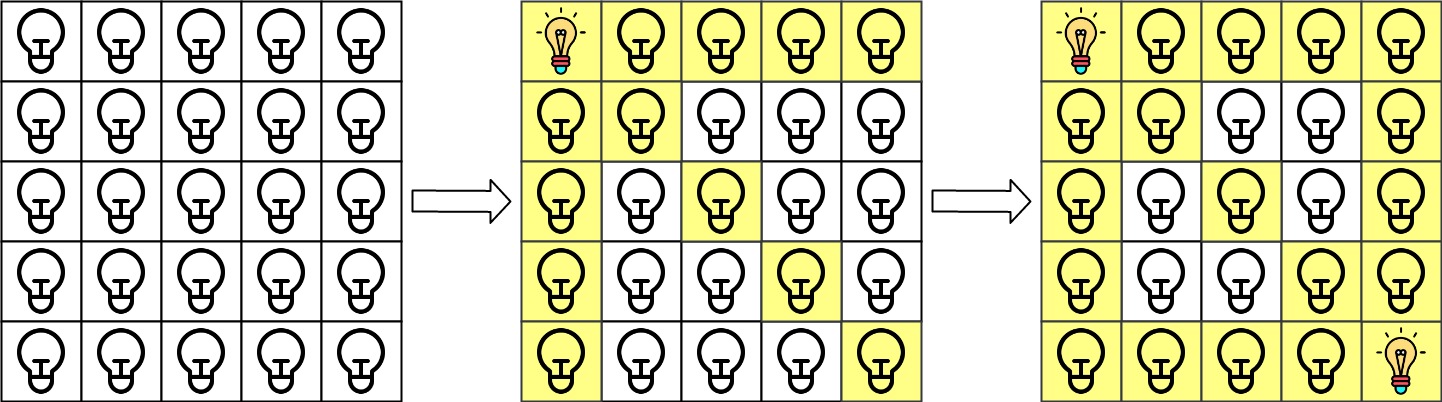
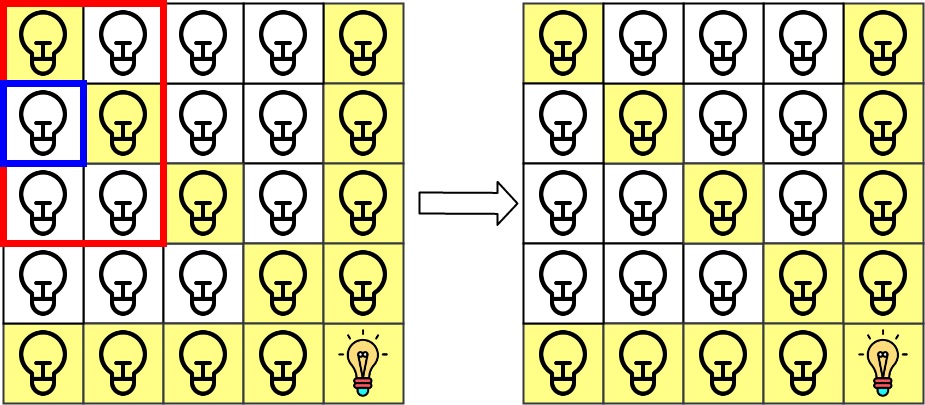
Input: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]
Output: [1,0]
Explanation: We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid[0][0] then turning on the lamp at grid[4][4].
The 0th query asks if the lamp at grid[1][1] is illuminated or not (the blue square). It is illuminated, so set ans[0] = 1. Then, we turn off all lamps in the red square.

The 1st query asks if the lamp at grid[1][0] is illuminated or not (the blue square). It is not illuminated, so set ans[1] = 0. Then, we turn off all lamps in the red rectangle.

Example 2:

Input: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]
Output: [1,1]

Example 3:

Input: n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]
Output: [1,1,0]

 

Constraints:

  • 1 <= n <= 109
  • 0 <= lamps.length <= 20000
  • 0 <= queries.length <= 20000
  • lamps[i].length == 2
  • 0 <= rowi, coli < n
  • queries[j].length == 2
  • 0 <= rowj, colj < n

Solution Explanation: Grid Illumination

This problem involves determining whether specific cells in a grid are illuminated by a set of lamps, given a series of queries. The challenge lies in the large grid size (up to 109 x 109) and the efficient handling of lamp illumination and subsequent lamp removal.

Core Idea: Instead of explicitly representing the entire grid, which would be infeasible due to its size, we leverage the observation that a lamp illuminates an entire row, column, and both diagonals passing through it. We can track the number of lamps affecting each row, column, and diagonal using hash maps (dictionaries).

Algorithm:

  1. Lamp Initialization:

    • We use a set (or HashSet) s to store the unique lamp positions to avoid duplicate processing.

    • We use four Counter objects (or HashMaps) to track the number of lamps affecting each:

      • row: Number of lamps in each row.
      • col: Number of lamps in each column.
      • diag1: Number of lamps on each main diagonal (where row == col).
      • diag2: Number of lamps on each anti-diagonal (where row + col is constant).

    • For each lamp (i, j) in lamps, we increment the counts in the corresponding row[i], col[j], diag1[i - j], and diag2[i + j].

  2. Query Processing:

    • For each query (i, j) in queries:
      • We check if the cell is illuminated by any lamp: If row[i] > 0, col[j] > 0, diag1[i - j] > 0, or diag2[i + j] > 0, the cell is illuminated; we add 1 to the answer array.
      • We simulate turning off the lamp at (i, j) and its 8 neighbors:
        • Iterate through the 3x3 area around (i, j).
        • If a lamp exists at (x, y) within this area, remove it from s and decrement the counts in the corresponding row, col, diag1, and diag2.

  3. Return Answer: The answer array containing 1 (illuminated) or 0 (not illuminated) for each query is returned.

Time Complexity:

  • The initialization step takes O(m), where m is the number of lamps.
  • Query processing takes O(q * 9), where q is the number of queries. The 9 comes from checking the 3x3 neighbor area. This simplifies to O(q).
  • Therefore, the overall time complexity is O(m + q).

Space Complexity:

  • The space used is dominated by the hash maps, which store at most O(m + n) entries (where n is the number of rows/columns, it will be dominated by 'm' usually), in the worst case.
  • The set s can store at most m elements.
  • Thus, the overall space complexity is O(m + n). In practice, O(m) dominates if the grid is significantly larger than the number of lamps.

Code Examples (Python):

The Python code using collections.Counter efficiently handles the counting and updating of lamps affecting each row, column, and diagonal.

Note: The provided Java, C++, Go, and TypeScript codes follow the same algorithmic approach, adapting the data structures to the specific language. They effectively manage the large grid implicitly using hash maps/dictionaries. The use of long long or similar data types in C++ and Java is important for handling the potentially large n value without integer overflow.