{x}
blog image

Maximum Binary Tree II

A maximum tree is a tree where every node has a value greater than any other value in its subtree.

You are given the root of a maximum binary tree and an integer val.

Just as in the previous problem, the given tree was constructed from a list a (root = Construct(a)) recursively with the following Construct(a) routine:

  • If a is empty, return null.
  • Otherwise, let a[i] be the largest element of a. Create a root node with the value a[i].
  • The left child of root will be Construct([a[0], a[1], ..., a[i - 1]]).
  • The right child of root will be Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]]).
  • Return root.

Note that we were not given a directly, only a root node root = Construct(a).

Suppose b is a copy of a with the value val appended to it. It is guaranteed that b has unique values.

Return Construct(b).

 

Example 1:

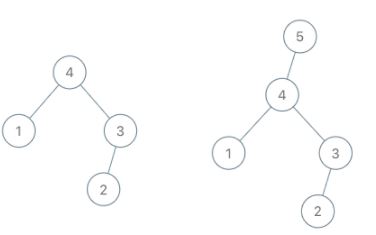
Input: root = [4,1,3,null,null,2], val = 5
Output: [5,4,null,1,3,null,null,2]
Explanation: a = [1,4,2,3], b = [1,4,2,3,5]

Example 2:

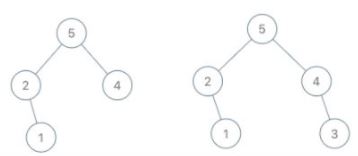
Input: root = [5,2,4,null,1], val = 3
Output: [5,2,4,null,1,null,3]
Explanation: a = [2,1,5,4], b = [2,1,5,4,3]

Example 3:

Input: root = [5,2,3,null,1], val = 4
Output: [5,2,4,null,1,3]
Explanation: a = [2,1,5,3], b = [2,1,5,3,4]

 

Constraints:

  • The number of nodes in the tree is in the range [1, 100].
  • 1 <= Node.val <= 100
  • All the values of the tree are unique.
  • 1 <= val <= 100

Solution Explanation for LeetCode 998: Maximum Binary Tree II

This problem asks to insert a new node with value val into a maximum binary tree. A maximum binary tree is a tree where every node's value is greater than any node in its subtree. The insertion should maintain this maximum tree property.

Approach 1: Recursive Solution

This approach leverages the recursive nature of constructing a maximum binary tree. We recursively traverse the tree, looking for the appropriate place to insert the new node.

Algorithm:

  1. Base Case: If the current node is null or its value is less than val, create a new node with val and make the current node its left child. This new node becomes the new root of the subtree.
  2. Recursive Step: Otherwise, recursively call the function on the right subtree with val. This ensures that val is inserted into the correct position within the right subtree, maintaining the maximum tree property.

Time Complexity: O(N), where N is the number of nodes in the tree. This is because in the worst case we traverse the entire tree. Space Complexity: O(N) in the worst case due to the recursive call stack. The recursion depth can be at most N if the tree is skewed.

Approach 2: Iterative Solution

This approach avoids recursion by iteratively traversing the tree to find the correct insertion point.

Algorithm:

  1. Base Case: If the root's value is less than val, create a new node with val and make the root its left child. This is the new root.
  2. Iteration: Otherwise, start at the root and traverse the right subtree. As long as we encounter nodes with values greater than val, continue traversing to the right.
  3. Insertion: When we find a node whose right child's value is less than or equal to val, create a new node with val, make the current node's right child the left child of the new node, and then set the new node as the current node's right child.

Time Complexity: O(N), where N is the number of nodes in the tree. In the worst case, we might traverse the entire right branch. Space Complexity: O(1). We are using only a constant number of extra variables.

Code Examples (Python)

Approach 1 (Recursive):

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
 
class Solution:
    def insertIntoMaxTree(self, root: TreeNode, val: int) -> TreeNode:
        if not root or root.val < val:
            return TreeNode(val, root)
        root.right = self.insertIntoMaxTree(root.right, val)
        return root

Approach 2 (Iterative):

class Solution:
    def insertIntoMaxTree(self, root: TreeNode, val: int) -> TreeNode:
        if not root or root.val < val:
            return TreeNode(val, root)
        curr = root
        node = TreeNode(val)
        while curr.right and curr.right.val > val:
            curr = curr.right
        node.left = curr.right
        curr.right = node
        return root

The code examples in other languages (Java, C++, Go, TypeScript, Rust, C) follow similar logic, reflecting the algorithms described above. The choice between the recursive and iterative approach is often a matter of preference and potential considerations about stack overflow in very deep trees (favoring iterative in those scenarios). Both have the same asymptotic time complexity.