- {x}
- Calculate Digit Sum of a String
- Minimum Rounds to Complete All Tasks
- Maximum Trailing Zeros in a Cornered Path
- Longest Path With Different Adjacent Characters
- Maximum Cost of Trip With K Highways
- Intersection of Multiple Arrays
- Count Lattice Points Inside a Circle
- Count Number of Rectangles Containing Each Point
- Number of Flowers in Full Bloom
- Dynamic Pivoting of a Table
- Dynamic Unpivoting of a Table
- Design Video Sharing Platform
- Count Prefixes of a Given String
- Minimum Average Difference
- Count Unguarded Cells in the Grid
- Escape the Spreading Fire
- Remove Digit From Number to Maximize Result
- Read More...

Number of Flowers in Full Bloom
You are given a 0-indexed 2D integer array flowers, where flowers[i] = [starti, endi] means the ith flower will be in full bloom from starti to endi (inclusive). You are also given a 0-indexed integer array people of size n, where people[i] is the time that the ith person will arrive to see the flowers.
Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the ith person arrives.
Example 1:
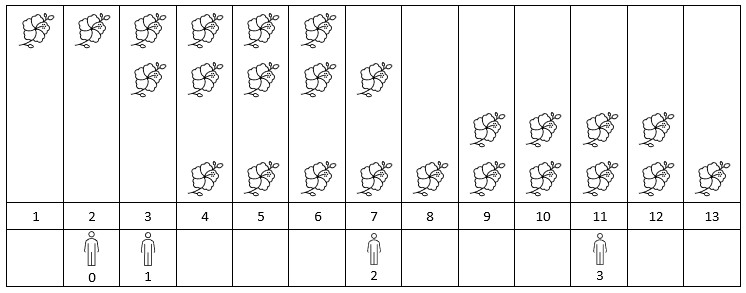
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11] Output: [1,2,2,2] Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive. For each person, we return the number of flowers in full bloom during their arrival.
Example 2:
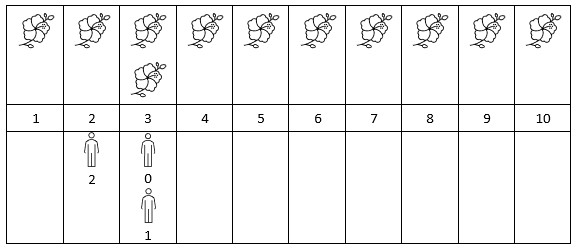
Input: flowers = [[1,10],[3,3]], people = [3,3,2] Output: [2,2,1] Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive. For each person, we return the number of flowers in full bloom during their arrival.
Constraints:
1 <= flowers.length <= 5 * 104flowers[i].length == 21 <= starti <= endi <= 1091 <= people.length <= 5 * 1041 <= people[i] <= 109
Solution Explanation: Number of Flowers in Full Bloom
This problem asks to find the number of flowers in full bloom for each person's arrival time. The most efficient solutions leverage sorting and binary search or a difference array for optimal time complexity. Let's explore both approaches.
Approach 1: Sorting + Binary Search
-
Data Preparation:
- Create two sorted arrays:
start_timesandend_times.start_timescontains the start times of all flowers, sorted in ascending order.end_timescontains the end times of all flowers, also sorted in ascending order.
- Create two sorted arrays:
-
Querying for Each Person:
- For each person's arrival time
p:- Use binary search on
start_timesto find the indexrsuch thatstart_times[r] <= p. This represents the number of flowers that have started blooming by timep. - Use binary search on
end_timesto find the indexlsuch thatend_times[l] < p. This represents the number of flowers that have already wilted by timep. - The number of flowers in bloom at time
pisr - l.
- Use binary search on
- For each person's arrival time
Time Complexity Analysis:
- Sorting
start_timesandend_times: O(m log m), where m is the number of flowers. - Binary search for each person: O(n log m), where n is the number of people.
- Total Time Complexity: O((m + n) log m)
Space Complexity Analysis:
start_timesandend_timesarrays: O(m) space.- Total Space Complexity: O(m)
Approach 2: Difference Array + Sorting + Offline Query
-
Difference Array:
- Create a difference array
diff(a map or dictionary) to store the changes in the number of blooming flowers at each time point. - For each flower
[start, end], incrementdiff[start]by 1 (a new flower blooms) and decrementdiff[end + 1]by 1 (the flower wilts).
- Create a difference array
-
Sorting and Offline Query:
- Sort the
peoplearray by arrival time. - Iterate through the sorted
peoplearray. For each person:- Iterate through the
diffarray (sorted by keys) until the current time exceeds the person's arrival time. - Accumulate the values in
diff(representing the total number of blooming flowers) until you reach the person's arrival time. This gives you the number of flowers in bloom for that person.
- Iterate through the
- Sort the
Time Complexity Analysis:
- Creating the difference array: O(m)
- Sorting
people: O(n log n) - Iterating through sorted
peopleanddiff: O(m + n) in the best case (assuming mostly unique arrival times and flower bloom durations), potentially O(m*n) in the worst case if many overlaps occur - Total Time Complexity: O(m + n log n) or O(m*n)
Space Complexity Analysis:
diffarray: O(m)- Sorted
people: O(n) - Total Space Complexity: O(m + n)
Code Examples (Python):
Approach 1 (Sorting + Binary Search):
import bisect
def fullBloomFlowers(flowers, people):
start_times = sorted([start for start, _ in flowers])
end_times = sorted([end for _, end in flowers])
result = []
for person_time in people:
blooming_flowers = bisect.bisect_right(start_times, person_time) - bisect.bisect_left(end_times, person_time)
result.append(blooming_flowers)
return result
Approach 2 (Difference Array):
from collections import defaultdict
def fullBloomFlowers(flowers, people):
diff = defaultdict(int)
for start, end in flowers:
diff[start] += 1
diff[end + 1] -= 1
sorted_times = sorted(diff.keys())
sorted_people_with_indices = sorted(enumerate(people), key=lambda x: x[1])
result = [0] * len(people)
blooming_count = 0
time_index = 0
for person_index, person_time in sorted_people_with_indices:
while time_index < len(sorted_times) and sorted_times[time_index] <= person_time:
blooming_count += diff[sorted_times[time_index]]
time_index += 1
result[person_index] = blooming_count
return result
The choice between these approaches depends on the expected distribution of input data. If m (number of flowers) is significantly larger than n (number of people), Approach 1 might be slightly faster. If n is larger or comparable to m, and the distribution of flower bloom times and arrival times is relatively spread out, Approach 2 could be faster. If there are many overlaps, Approach 2 could be slower. However, Approach 2 generally uses less space. Consider the constraints and expected inputs when selecting an approach.