{x}
blog image

Count Number of Rectangles Containing Each Point

You are given a 2D integer array rectangles where rectangles[i] = [li, hi] indicates that ith rectangle has a length of li and a height of hi. You are also given a 2D integer array points where points[j] = [xj, yj] is a point with coordinates (xj, yj).

The ith rectangle has its bottom-left corner point at the coordinates (0, 0) and its top-right corner point at (li, hi).

Return an integer array count of length points.length where count[j] is the number of rectangles that contain the jth point.

The ith rectangle contains the jth point if 0 <= xj <= li and 0 <= yj <= hi. Note that points that lie on the edges of a rectangle are also considered to be contained by that rectangle.

 

Example 1:

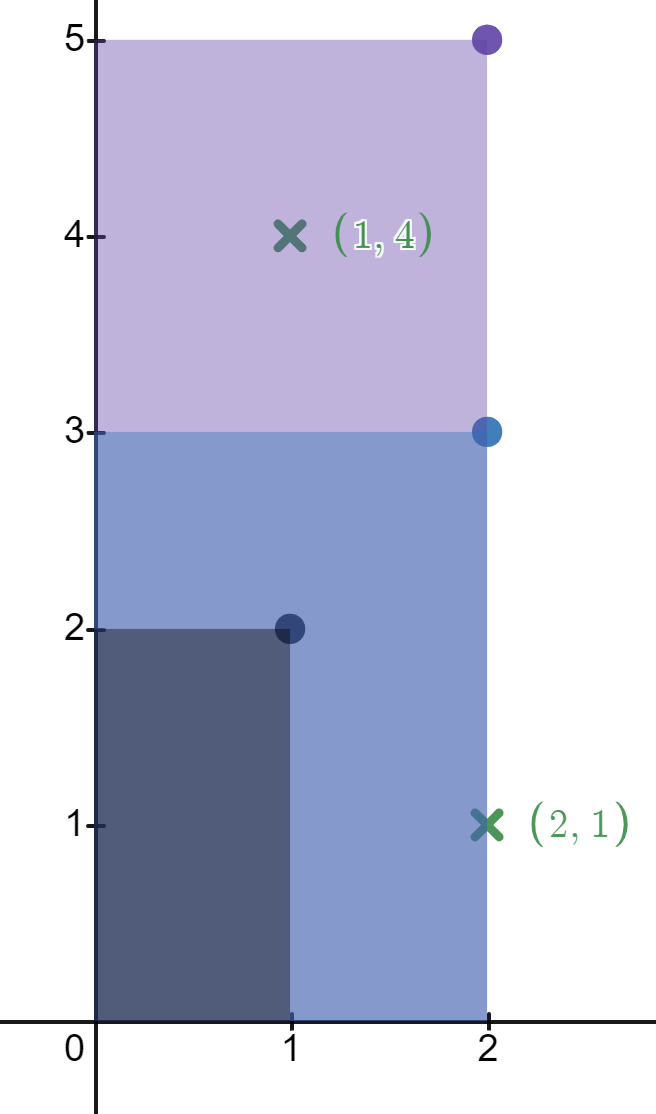
Input: rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]]
Output: [2,1]
Explanation: 
The first rectangle contains no points.
The second rectangle contains only the point (2, 1).
The third rectangle contains the points (2, 1) and (1, 4).
The number of rectangles that contain the point (2, 1) is 2.
The number of rectangles that contain the point (1, 4) is 1.
Therefore, we return [2, 1].

Example 2:

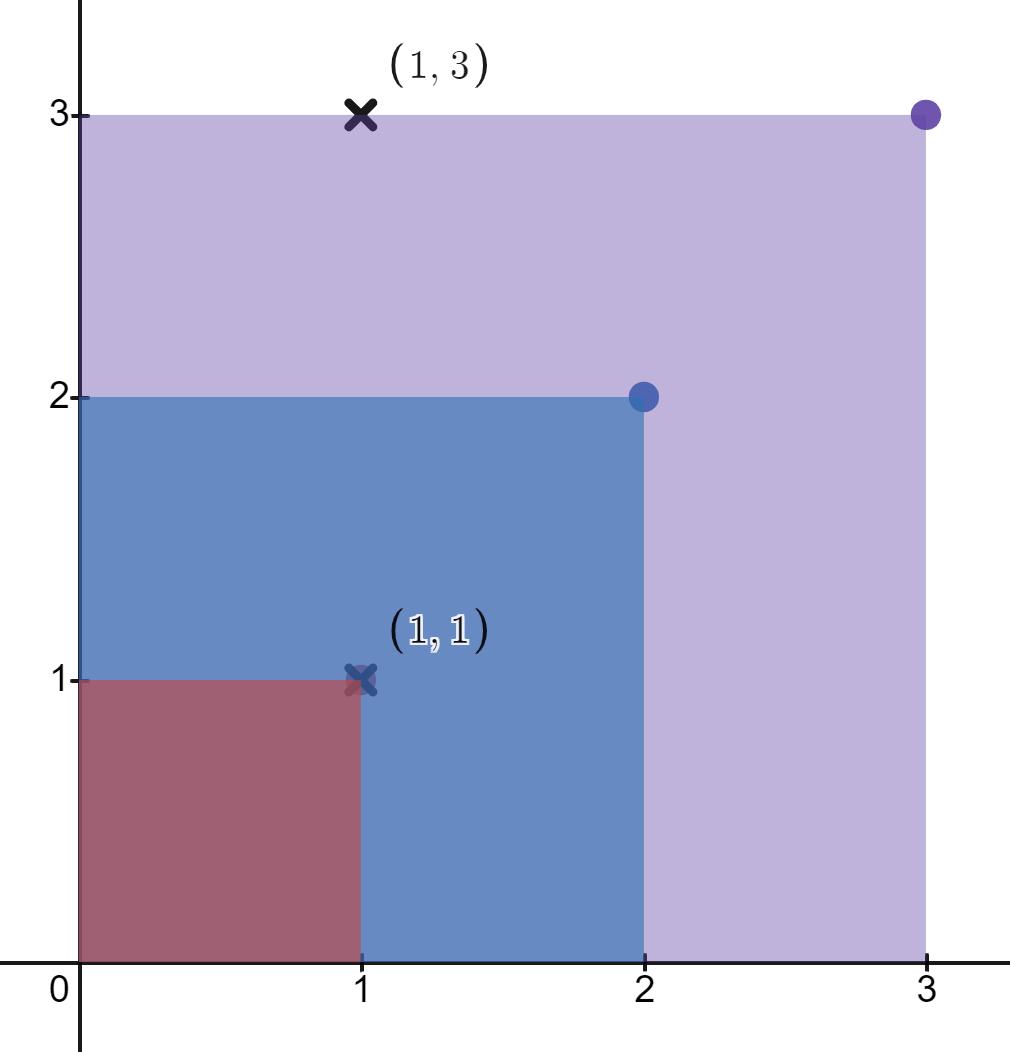
Input: rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]]
Output: [1,3]
Explanation:
The first rectangle contains only the point (1, 1).
The second rectangle contains only the point (1, 1).
The third rectangle contains the points (1, 3) and (1, 1).
The number of rectangles that contain the point (1, 3) is 1.
The number of rectangles that contain the point (1, 1) is 3.
Therefore, we return [1, 3].

 

Constraints:

  • 1 <= rectangles.length, points.length <= 5 * 104
  • rectangles[i].length == points[j].length == 2
  • 1 <= li, xj <= 109
  • 1 <= hi, yj <= 100
  • All the rectangles are unique.
  • All the points are unique.

Solution Explanation

This problem asks us to count the number of rectangles that contain each point in a given set of points. The solution uses a combination of sorting and binary search for efficient computation.

Approach:

  1. Organize Rectangles by Height: We create a dictionary (or map in other languages) where the keys are the heights of the rectangles, and the values are lists of the lengths of rectangles with that height. This pre-processing step allows us to quickly find rectangles of a given height.

  2. Sort Lengths: For each height in our dictionary, we sort the list of lengths in ascending order. This is crucial for efficient binary search in the next step.

  3. Count Rectangles for Each Point: For each point (x, y), we iterate through heights starting from the point's y-coordinate up to the maximum height (100). For each height h:

    • We perform a binary search on the sorted list of lengths for that height to find the index of the first length greater than or equal to x.
    • The number of rectangles with height h that contain the point (x, y) is the total number of lengths minus the index found by the binary search. This is because all lengths at indices greater than or equal to the found index are greater than or equal to x.

  4. Accumulate Counts: The total count of rectangles containing a point is accumulated by summing the counts for each height. This is added to our result list.

Time Complexity:

  • Pre-processing: Sorting the lengths for each height takes O(N log N) time in the worst case, where N is the number of rectangles. The creation of the height-length dictionary takes O(N) time.
  • Point Processing: For each point, we iterate through at most 100 heights. The binary search in each height takes O(log M) time where M is the maximum number of rectangles with a specific height. Therefore, the time complexity for processing points is O(P * 100 * log M), where P is the number of points. In the worst case, M could be N (all rectangles have the same height), making this O(P * 100 * log N).

Overall Time Complexity: O(N log N + P * 100 * log N). Since 100 is a constant, we can simplify to O(N log N + P log N). If N and P are of the same order, this further simplifies to O(N log N).

Space Complexity: O(N) to store the height-length dictionary. The space used for sorting is usually in-place or uses a small amount of auxiliary space, which is negligible compared to O(N).

Code Explanations (Python):

The Python code uses defaultdict for the height-length dictionary which handles empty lists efficiently. bisect_left performs the binary search. The main loop iterates through points and heights, and the binary search efficiently finds the number of rectangles containing each point.

Code Explanations (Java, C++, Go, TypeScript):

The Java, C++, Go, and TypeScript codes follow a similar approach. They use appropriate data structures (e.g., ArrayList, vector, []int, arrays) and functions (e.g., Collections.sort, sort, sort.Ints, sort) to achieve the same functionality as the Python code. The binary search is implemented using a while loop. The logic remains consistent across all languages, although specific syntax and library functions vary.