- {x}
- Palindrome Removal
- Minimum Swaps to Make Strings Equal
- Count Number of Nice Subarrays
- Minimum Remove to Make Valid Parentheses
- Check If It Is a Good Array
- Average Selling Price
- Cells with Odd Values in a Matrix
- Reconstruct a 2-Row Binary Matrix
- Number of Closed Islands
- Maximum Score Words Formed by Letters
- Encode Number
- Smallest Common Region
- Synonymous Sentences
- Handshakes That Don't Cross
- Shift 2D Grid
- Find Elements in a Contaminated Binary Tree
- Greatest Sum Divisible by Three
- Read More...

Number of Closed Islands
Given a 2D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.
Return the number of closed islands.
Example 1:
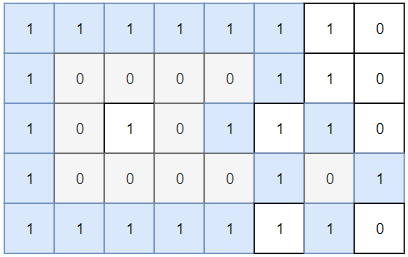
Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]] Output: 2 Explanation: Islands in gray are closed because they are completely surrounded by water (group of 1s).
Example 2:
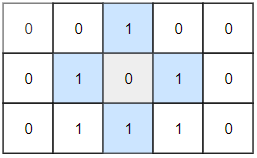
Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]] Output: 1
Example 3:
Input: grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
Output: 2
Constraints:
1 <= grid.length, grid[0].length <= 1000 <= grid[i][j] <=1
1254. Number of Closed Islands
Problem Description
Given a 2D grid representing land (0) and water (1), find the number of closed islands. A closed island is a maximal 4-directionally connected group of 0s (land) completely surrounded by 1s (water).
Solutions
Two approaches are presented: Depth-First Search (DFS) and Union-Find.
Solution 1: Depth-First Search (DFS)
This approach uses DFS to identify and count closed islands.
Algorithm:
- Iterate: Traverse the grid.
- DFS Function: For each cell with value 0 (land), call a recursive DFS function.
- Mark the current cell as visited (change its value to 1).
- Recursively call DFS on its four neighbors (up, down, left, right) if they are land (0).
- Boundary Check: The DFS function returns
trueif the island is closed (completely surrounded by water), andfalseotherwise. This is determined by checking if any visited land cell is on the boundary of the grid. - Count Islands: Increment the count of closed islands if the DFS function returns
true.
Time Complexity: O(M * N), where M and N are the dimensions of the grid. Each cell is visited at most once. Space Complexity: O(M * N) in the worst case, due to the recursive call stack during DFS (depth of recursion can be at most M*N).
Code (Python):
class Solution:
def closedIsland(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
def dfs(i, j):
if not (0 <= i < m and 0 <= j < n and grid[i][j] == 0):
return False # Out of bounds or water
grid[i][j] = 1 # Mark as visited (water)
is_closed = True
is_closed &= dfs(i + 1, j)
is_closed &= dfs(i - 1, j)
is_closed &= dfs(i, j + 1)
is_closed &= dfs(i, j - 1)
return is_closed
count = 0
for i in range(m):
for j in range(n):
if grid[i][j] == 0:
if dfs(i, j):
count += 1
return countSolution 2: Union-Find
This approach uses a Union-Find data structure to efficiently group connected land cells.
Algorithm:
- Union-Find Setup: Create a Union-Find data structure to represent the connectivity of land cells.
- Initial Unions: Iterate through the grid. For cells on the boundary that are land (0), unite them with a virtual "boundary" node. This ensures that islands touching the boundary are not considered closed.
- Internal Unions: For land cells that are not on the boundary, unite them with their adjacent land cells (up, down, left, right).
- Count Closed Islands: Iterate through the grid again. If a land cell's root (in the Union-Find) is the cell itself (not united with the boundary), it represents a closed island. Increment the count accordingly.
Time Complexity: O(M * N * α(M * N)), where α is the inverse Ackermann function, which grows extremely slowly and can be considered practically constant for all realistic input sizes. The dominant operation is the union and find operations in the Union-Find data structure. Space Complexity: O(M * N) to store the Union-Find data structure.
Code (Python):
class UnionFind:
def __init__(self, n):
self.parent = list(range(n))
self.size = [1] * n
def find(self, i):
if self.parent[i] == i:
return i
self.parent[i] = self.find(self.parent[i])
return self.parent[i]
def union(self, i, j):
root_i = self.find(i)
root_j = self.find(j)
if root_i != root_j:
if self.size[root_i] < self.size[root_j]:
root_i, root_j = root_j, root_i
self.parent[root_j] = root_i
self.size[root_i] += self.size[root_j]
class Solution:
def closedIsland(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
uf = UnionFind(m * n + 1) # +1 for the boundary node
boundary_node = m * n
for i in range(m):
for j in range(n):
if grid[i][j] == 0:
if i == 0 or i == m - 1 or j == 0 or j == n - 1:
uf.union(i * n + j, boundary_node)
else:
for x, y in [(i + 1, j), (i - 1, j), (i, j + 1), (i, j - 1)]:
if grid[x][y] == 0:
uf.union(i * n + j, x * n + y)
count = 0
for i in range(m):
for j in range(n):
if grid[i][j] == 0 and uf.find(i * n + j) != boundary_node:
count += 1
return count
Both solutions correctly solve the problem. The choice depends on the specific needs of the application. DFS is generally simpler to implement, while Union-Find might offer better performance for extremely large grids due to its amortized time complexity. However, the difference in performance is unlikely to be significant for most practical problem sizes.