- {x}
- Design A Leaderboard
- Tree Diameter
- Palindrome Removal
- Minimum Swaps to Make Strings Equal
- Count Number of Nice Subarrays
- Minimum Remove to Make Valid Parentheses
- Check If It Is a Good Array
- Average Selling Price
- Cells with Odd Values in a Matrix
- Reconstruct a 2-Row Binary Matrix
- Number of Closed Islands
- Maximum Score Words Formed by Letters
- Encode Number
- Smallest Common Region
- Synonymous Sentences
- Handshakes That Don't Cross
- Shift 2D Grid
- Read More...

Cells with Odd Values in a Matrix
There is an m x n matrix that is initialized to all 0's. There is also a 2D array indices where each indices[i] = [ri, ci] represents a 0-indexed location to perform some increment operations on the matrix.
For each location indices[i], do both of the following:
- Increment all the cells on row
ri. - Increment all the cells on column
ci.
Given m, n, and indices, return the number of odd-valued cells in the matrix after applying the increment to all locations in indices.
Example 1:
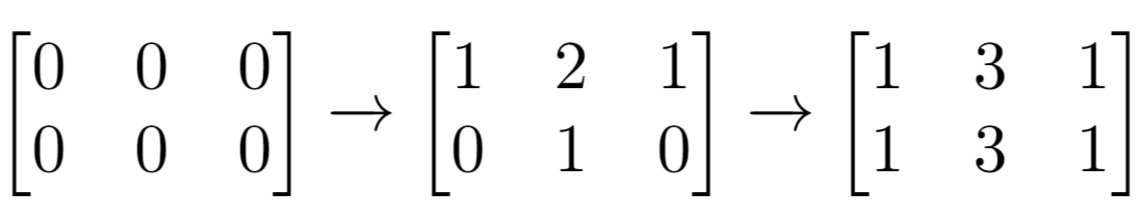
Input: m = 2, n = 3, indices = [[0,1],[1,1]] Output: 6 Explanation: Initial matrix = [[0,0,0],[0,0,0]]. After applying first increment it becomes [[1,2,1],[0,1,0]]. The final matrix is [[1,3,1],[1,3,1]], which contains 6 odd numbers.
Example 2:
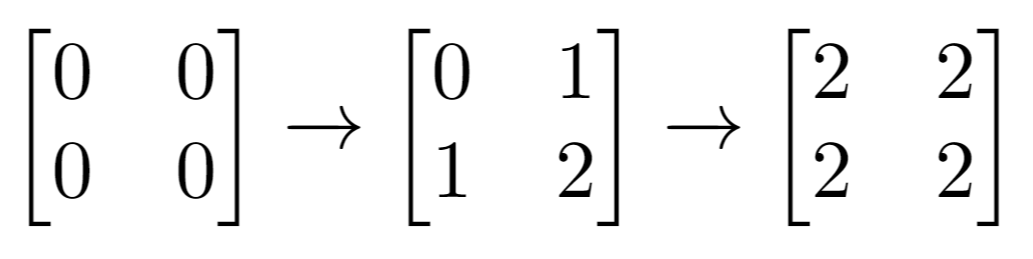
Input: m = 2, n = 2, indices = [[1,1],[0,0]] Output: 0 Explanation: Final matrix = [[2,2],[2,2]]. There are no odd numbers in the final matrix.
Constraints:
1 <= m, n <= 501 <= indices.length <= 1000 <= ri < m0 <= ci < n
Follow up: Could you solve this in O(n + m + indices.length) time with only O(n + m) extra space?
Solution Explanation for 1252. Cells with Odd Values in a Matrix
This problem involves a matrix initialized with zeros and a series of operations that increment rows and columns based on given indices. The goal is to efficiently count the number of cells with odd values after all operations.
Core Idea: Instead of explicitly creating and modifying the matrix (which would be inefficient for large matrices), we can track the number of times each row and column is incremented. The final value of a cell (i, j) will be the sum of increments to row i and column j.
Three Approaches:
The problem can be solved in three ways, each with different time and space complexities:
1. Simulation:
- Approach: This is the most straightforward approach. We create the matrix and simulate the increment operations directly. After all increments, we iterate through the matrix, counting odd-valued cells.
- Time Complexity: O(k(m+n) + mn), where k is the length of
indices, m is the number of rows, and n is the number of columns. The dominant factor is the nested loops for incrementing and counting. - Space Complexity: O(mn) because we create and store the entire matrix.
2. Space Optimization:
- Approach: Instead of creating the entire matrix, we maintain two arrays:
rowandcol.row[i]stores the number of times rowiis incremented, and similarly for columns. The value of a cell (i, j) is thenrow[i] + col[j]. We iterate through all possible cell indices and count odd values. - Time Complexity: O(k + mn). Creating
rowandcoltakes O(m+n), the loop for increments takes O(k), and the final counting loop takes O(mn). - Space Complexity: O(m+n) since we only store the
rowandcolarrays.
3. Mathematical Optimization:
- Approach: This is the most efficient approach. We observe that a cell (i, j) is odd only if exactly one of
row[i]andcol[j]is odd. We count odd rows (cnt1) and odd columns (cnt2). The number of odd cells is thencnt1 * (n - cnt2) + cnt2 * (m - cnt1). - Time Complexity: O(k + m + n). Counting increments takes O(k), and counting odd rows and columns takes O(m+n).
- Space Complexity: O(m+n) to store
rowandcolarrays.
Code Examples (Python):
Approach 1 (Simulation):
class Solution:
def oddCells(self, m: int, n: int, indices: List[List[int]]) -> int:
matrix = [[0] * n for _ in range(m)]
for r, c in indices:
for i in range(m):
matrix[i][c] += 1
for j in range(n):
matrix[r][j] += 1
count = 0
for row in matrix:
for cell in row:
if cell % 2 != 0:
count += 1
return count
Approach 2 (Space Optimization):
class Solution:
def oddCells(self, m: int, n: int, indices: List[List[int]]) -> int:
row_inc = [0] * m
col_inc = [0] * n
for r, c in indices:
row_inc[r] += 1
col_inc[c] += 1
count = 0
for i in range(m):
for j in range(n):
if (row_inc[i] + col_inc[j]) % 2 != 0:
count += 1
return count
Approach 3 (Mathematical Optimization):
class Solution:
def oddCells(self, m: int, n: int, indices: List[List[int]]) -> int:
row_inc = [0] * m
col_inc = [0] * n
for r, c in indices:
row_inc[r] += 1
col_inc[c] += 1
odd_rows = sum(1 for x in row_inc if x % 2 != 0)
odd_cols = sum(1 for x in col_inc if x % 2 != 0)
return odd_rows * (n - odd_cols) + odd_cols * (m - odd_rows)
The mathematical optimization (Approach 3) provides the best time complexity, making it the most efficient solution for large input sizes. The other approaches are provided for comparison and illustrative purposes. The space complexity is similar for approaches 2 and 3. Approach 1 is significantly less efficient in both time and space for large inputs.