{x}
blog image

Minimum Time Visiting All Points

On a 2D plane, there are n points with integer coordinates points[i] = [xi, yi]. Return the minimum time in seconds to visit all the points in the order given by points.

You can move according to these rules:

  • In 1 second, you can either:
    • move vertically by one unit,
    • move horizontally by one unit, or
    • move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in 1 second).
  • You have to visit the points in the same order as they appear in the array.
  • You are allowed to pass through points that appear later in the order, but these do not count as visits.

 

Example 1:

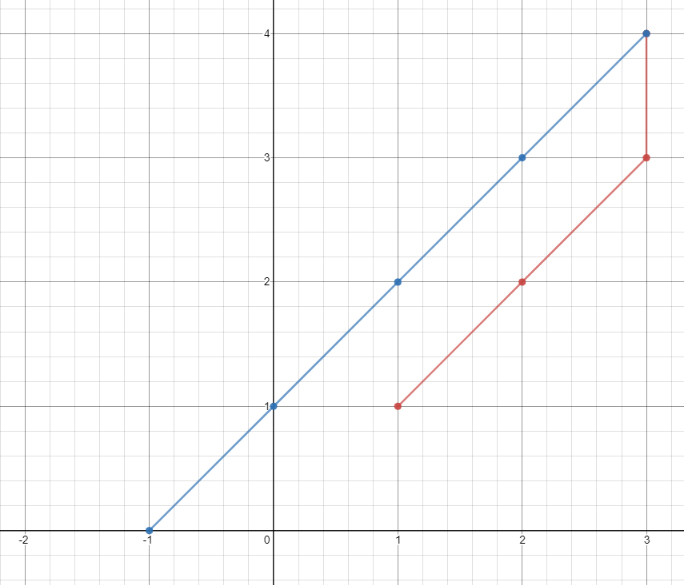
Input: points = [[1,1],[3,4],[-1,0]]
Output: 7
Explanation: One optimal path is [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]   
Time from [1,1] to [3,4] = 3 seconds 
Time from [3,4] to [-1,0] = 4 seconds
Total time = 7 seconds

Example 2:

Input: points = [[3,2],[-2,2]]
Output: 5

 

Constraints:

  • points.length == n
  • 1 <= n <= 100
  • points[i].length == 2
  • -1000 <= points[i][0], points[i][1] <= 1000

Minimum Time Visiting All Points

This problem involves finding the minimum time to visit a series of points in a 2D plane, given constraints on movement. We can move one unit vertically, one unit horizontally, or diagonally (one unit in each direction) in one second.

Approach

The key insight is that the minimum time to travel between two points (x1, y1) and (x2, y2) is the maximum of the absolute differences in their x and y coordinates: max(|x2 - x1|, |y2 - y1|). This is because we can always choose a path that uses diagonal moves as much as possible to minimize the time.

The solution iterates through the pairs of consecutive points, calculates the minimum time to travel between each pair using the formula above, and sums up these times.

Time and Space Complexity

  • Time Complexity: O(n), where n is the number of points. We iterate through the points once.
  • Space Complexity: O(1). The algorithm uses a constant amount of extra space.

Code Implementation (Python)

from itertools import pairwise
 
class Solution:
    def minTimeToVisitAllPoints(self, points: list[list[int]]) -> int:
        total_time = 0
        for (x1, y1), (x2, y2) in pairwise(points):
            total_time += max(abs(x2 - x1), abs(y2 - y1))
        return total_time

The pairwise function from the itertools library efficiently generates pairs of consecutive elements in the list of points. This makes the code cleaner and more readable. If itertools isn't available (e.g., in some restricted coding environments), a manual loop can be used as demonstrated in the other language examples.

Code Implementation (Other Languages)

The same core logic is implemented in other languages below, demonstrating the adaptability of this approach:

Java:

class Solution {
    public int minTimeToVisitAllPoints(int[][] points) {
        int totalTime = 0;
        for (int i = 1; i < points.length; i++) {
            int dx = Math.abs(points[i][0] - points[i - 1][0]);
            int dy = Math.abs(points[i][1] - points[i - 1][1]);
            totalTime += Math.max(dx, dy);
        }
        return totalTime;
    }
}

C++:

class Solution {
public:
    int minTimeToVisitAllPoints(vector<vector<int>>& points) {
        int totalTime = 0;
        for (size_t i = 1; i < points.size(); ++i) {
            int dx = abs(points[i][0] - points[i - 1][0]);
            int dy = abs(points[i][1] - points[i - 1][1]);
            totalTime += max(dx, dy);
        }
        return totalTime;
    }
};

JavaScript:

/**
 * @param {number[][]} points
 * @return {number}
 */
var minTimeToVisitAllPoints = function(points) {
    let totalTime = 0;
    for (let i = 1; i < points.length; i++) {
        let dx = Math.abs(points[i][0] - points[i-1][0]);
        let dy = Math.abs(points[i][1] - points[i-1][1]);
        totalTime += Math.max(dx, dy);
    }
    return totalTime;
};

These examples all follow the same efficient O(n) time and O(1) space algorithm. The only variation is the syntax specific to each programming language.