- {x}
- Handshakes That Don't Cross
- Shift 2D Grid
- Find Elements in a Contaminated Binary Tree
- Greatest Sum Divisible by Three
- Minimum Moves to Move a Box to Their Target Location
- Page Recommendations
- Print Immutable Linked List in Reverse
- Minimum Time Visiting All Points
- Count Servers that Communicate
- Search Suggestions System
- Number of Ways to Stay in the Same Place After Some Steps
- All People Report to the Given Manager
- Hexspeak
- Remove Interval
- Delete Tree Nodes
- Number of Ships in a Rectangle
- Find Winner on a Tic Tac Toe Game
- Read More...

Count Servers that Communicate
You are given a map of a server center, represented as a m * n integer matrix grid, where 1 means that on that cell there is a server and 0 means that it is no server. Two servers are said to communicate if they are on the same row or on the same column.
Return the number of servers that communicate with any other server.
Example 1:
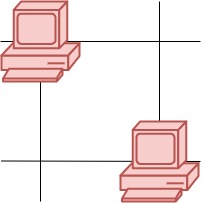
Input: grid = [[1,0],[0,1]] Output: 0 Explanation: No servers can communicate with others.
Example 2:
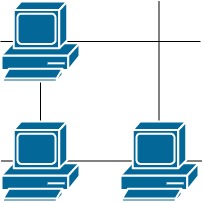
Input: grid = [[1,0],[1,1]] Output: 3 Explanation: All three servers can communicate with at least one other server.
Example 3:
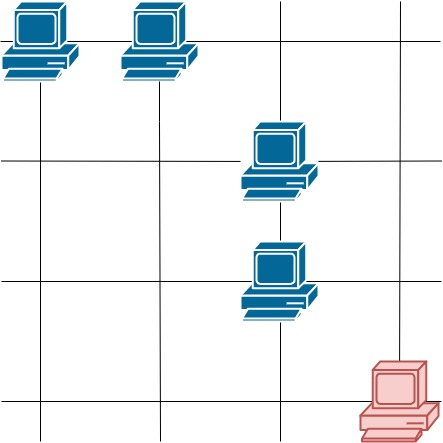
Input: grid = [[1,1,0,0],[0,0,1,0],[0,0,1,0],[0,0,0,1]] Output: 4 Explanation: The two servers in the first row can communicate with each other. The two servers in the third column can communicate with each other. The server at right bottom corner can't communicate with any other server.
Constraints:
m == grid.lengthn == grid[i].length1 <= m <= 2501 <= n <= 250grid[i][j] == 0 or 1
Solution Explanation: Counting Servers that Communicate
This problem asks to find the number of servers that can communicate with at least one other server. Two servers communicate if they are on the same row or column. The most efficient solution uses a counting approach.
Approach:
-
Count Row and Column Servers: We first iterate through the grid and count the number of servers in each row and each column. We store these counts in
rowandcolarrays respectively. -
Check Communication: We iterate through the grid again. For each server (represented by a
1in the grid), we check if either the count of servers in its row (row[i]) or the count of servers in its column (col[j]) is greater than 1. If either condition is true, it means the server can communicate with at least one other server, and we increment theanscounter. -
Return Count: Finally, we return the
answhich represents the total number of servers that can communicate.
Time Complexity Analysis:
The solution involves two nested loops to iterate through the grid (m x n size). Therefore, the time complexity is O(m*n), where 'm' is the number of rows and 'n' is the number of columns. This is linear with respect to the size of the input grid.
Space Complexity Analysis:
We use two arrays, row and col, to store the counts of servers in each row and column. The size of these arrays is m and n respectively. Therefore, the space complexity is O(m+n), which is linear with respect to the dimensions of the input grid. This is relatively small compared to the input size.
Code Examples:
The provided code examples in Python, Java, C++, Go, and TypeScript all implement this counting approach. They differ slightly in syntax but follow the same fundamental logic:
- Initialization: Arrays
rowandcolare initialized to store row and column counts. - Counting Phase: The first nested loop populates
rowandcol. - Communication Check: The second nested loop checks communication and updates the
anscounter. - Return Value: The function returns
ans.
The code is concise and efficiently solves the problem within the stated time and space complexity bounds. No more sophisticated data structures or algorithms (like Union Find) are necessary for this optimal solution.