{x}
blog image

Minimum Number of Food Buckets to Feed the Hamsters

You are given a 0-indexed string hamsters where hamsters[i] is either:

  • 'H' indicating that there is a hamster at index i, or
  • '.' indicating that index i is empty.

You will add some number of food buckets at the empty indices in order to feed the hamsters. A hamster can be fed if there is at least one food bucket to its left or to its right. More formally, a hamster at index i can be fed if you place a food bucket at index i - 1 and/or at index i + 1.

Return the minimum number of food buckets you should place at empty indices to feed all the hamsters or -1 if it is impossible to feed all of them.

 

Example 1:

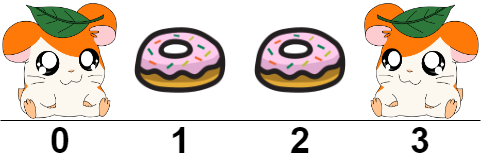
Input: hamsters = "H..H"
Output: 2
Explanation: We place two food buckets at indices 1 and 2.
It can be shown that if we place only one food bucket, one of the hamsters will not be fed.

Example 2:

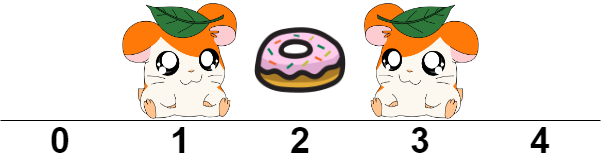
Input: hamsters = ".H.H."
Output: 1
Explanation: We place one food bucket at index 2.

Example 3:

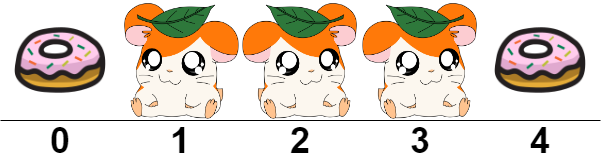
Input: hamsters = ".HHH."
Output: -1
Explanation: If we place a food bucket at every empty index as shown, the hamster at index 2 will not be able to eat.

 

Constraints:

  • 1 <= hamsters.length <= 105
  • hamsters[i] is either'H' or '.'.

Solution Explanation

This problem asks for the minimum number of food buckets needed to feed all hamsters, given a string representing the arrangement of hamsters ('H') and empty spaces ('.'). A hamster can be fed if there's a bucket to its left or right. The solution uses a greedy approach.

Greedy Approach:

The core idea is to iterate through the hamsters string. When we encounter a hamster ('H'), we try to place a bucket in the most efficient way possible:

  1. Check the right: If there's an empty space to the right (.) of the hamster, place a bucket there. This allows us to potentially feed this hamster and possibly the next one with a single bucket. Move the index i forward by 2 to skip over both the hamster and the placed bucket.

  2. Check the left: If there's no empty space to the right, but there's an empty space to the left, place the bucket to the left.

  3. Impossible case: If neither to the left nor right is empty, it's impossible to feed this hamster, so return -1.

Time Complexity Analysis:

The solution iterates through the string once. Therefore, the time complexity is O(n), where n is the length of the hamsters string.

Space Complexity Analysis:

The solution uses only a constant amount of extra space. Therefore, the space complexity is O(1).

Code Explanation (Python)

class Solution:
    def minimumBuckets(self, street: str) -> int:
        ans = 0
        i, n = 0, len(street)
        while i < n:
            if street[i] == 'H':
                if i + 1 < n and street[i + 1] == '.': #Check right
                    i += 2
                    ans += 1
                elif i and street[i - 1] == '.': #Check Left
                    ans += 1
                else:
                    return -1 #Impossible case
            i += 1
        return ans

The Python code directly implements the greedy strategy described above. It iterates through the street string. If it finds a hamster:

  • It checks if a bucket can be placed to the right. If so, it increments the bucket count (ans) and moves the index i forward by two.
  • Otherwise, it checks to the left. If possible, it places a bucket to the left, increments ans.
  • If neither is possible, it returns -1.

The other languages (Java, C++, Go) follow the same logic, just with the syntactic differences of those languages. The core algorithm and complexity analysis remain the same.